In einem Drachenviereck sind die Seiten a, b und der Winkel Alpha bekannt.

Question

Brauche unbedingt Hilfeee :/ :/

In einem Drachen sind die Seiten a, b und der Winkel Alpha bekannt. Alpha= 76° a= 7 cm b=13 cm A. Berechne die Länge der beiden Diagonalen e und f. B. Wie groß sind die Winkel Beta, Gamma und Delta. C. Berechne den Flächeninhalt.

Answer 1

In einem Drachenviereck  ist die Diagonale f Winkelhalbierende des Winkels alpha. So ergibt sich der in der Skizze eingezeichnete Wert von 38 °.
Außerdem schneiden sich die Diagonalen rechtwinklig, sodass also jedes der vier Teildreiecke, in die das Drachenviereck durch seine Diagonalen aufgeteilt wird, rechtwinklig ist.

Hier eine Skizze:

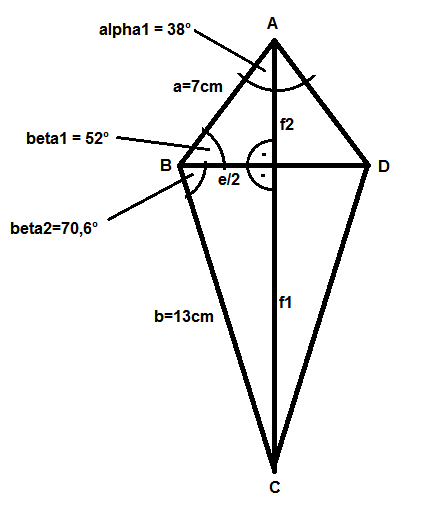
Berechnung der Längen der Diagonalen e und f

Es gilt:

1)

( e / 2 ) / 7 = sin ( 38 °)

<=> e = 14 * sin ( 38 ° ) = 8,62 cm

 

2)

f2 / 7 = sin ( 52 ° )

<=> f2 = 7 * sin ( 52 ° ) = 5,52 cm

 

3)  Mit dem Satz des Pythagoras:

f1 ² + ( e / 2 ) ² = 13 ² = 169

<=> f1 = √ ( 169 - 4,31 ² ) = 12,26 cm

Also:

f = f1 + f2 = 12,26 + 5,52 = 17,78 cm

 

Berechnung der Winkel:

sin ( beta2 ) = f1 / b = 12,26 / 13

<=> beta = arcsin ( 12,26 / 13 ) = 70,6 °

=> beta = beta1 + beta2 = 52 ° + 70,6 ° = 122,6 °

 

=> delta = beta = 122,6 °

=> gamma = 360 ° - alpha - beta - delta = 360 ° - 76 ° - 122,6 ° - 122,6 ° = 38,8°

 

Berechnung des Flächeninhaltes

A = e * f / 2 = 8,62 * 17,78 / 2 = 76,63 cm ²