Beweisführung am Parallelogramm

Question

für ein Parallelogramm existieren folgende Eigenschaften:

1. Gegenüberliegende Seiten sind gleich lang

2. Diagonal gegenüberliegende Winkel sind gleich groß

3. Die Summe der benachbarten Winkel ergibt 180 Grad

4. Die Diagonalen halbieren einander


Meine Frage: Ist der Beweis erbracht, wenn alle vier Behauptungen mathematisch belegt sind?

Answer 1

Ja, dann ist der Beweis erbracht.

Es gilt sogar: Ein nicht entartetes Viereck ist bereits dann ein Parallelogramm, wenn auch nur eine dieser 4  Bedingungen erfüllt ist.

Comments

Eine Frage zum Beweis für die erste Eigenschaft:

Eine mathematisches Gesetz lautet, dass zwei Geraden ( Seiten ) parallel sind, sobald die Wechselwinkel der Diagonale, welche die gegenüberliegenden Punkte schneidet, gleich groß sind ( s. Grafik )

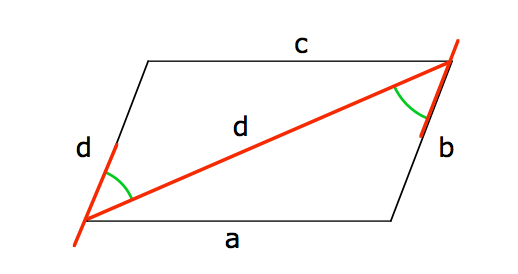
Nur dürfen die Jungs die Winkel nicht messen. Da jedoch feststeht, dass es sich um ein Parallelogramm handelt, müsste das Gesetz als Beweis dennoch gelten, oder?