Hallo Adile,
eine Geradengleichung lautet allgemein:
y = mx + b
wobei m den Anstieg bezeichnet und b den y-Achsenabschnitt.
Wenn wir zwei Punkte gegeben haben, setzen wir einfach ein:
25.)
a.) [P1(2,2), P2(3,3)]
y = (3-2)/(3-2)*x + b, also
y = x + b
Nun setzen wir nochmals einen Punkt, also zum Beispiel P1 ein:
2 = 2 + b
Also b = 0
Die Geradengleichung lautet demnach
y = x
25.)
b.) [P1(1,-3), P2(2,2)]
y = (2 - (-3))/(2-1)*x + b, also
y = 5 * x + b
Wir setzen einen Punkt, zum Beispiel P2 - der ist einfach - ein:
2 = 5 * 2 + b
Also b = -8
Die Geradengleichung lautet demnach
y = 5 * x - 8
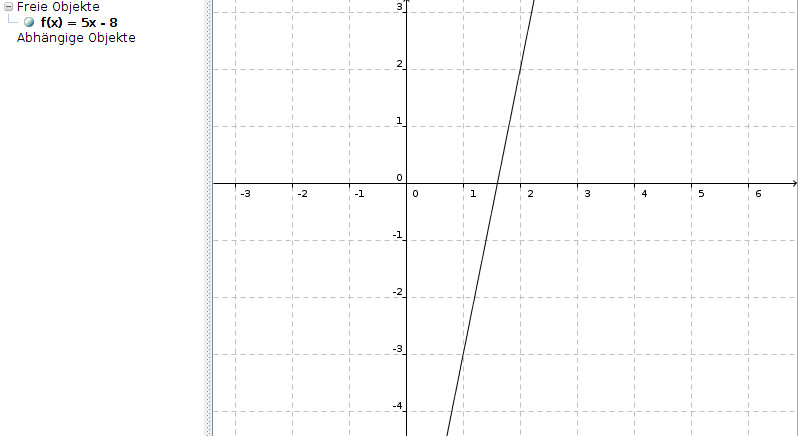
25.) Von einer Gerade g sind zwei Punkte bekannt.
c.) [(-1,-7), P2(2,-4)]
y = (-4 - (-7))/(2 - (-1)) * x + b, also
y = 3/3 * x + b
Wir setzen einen Punkt, zum Beispiel P2 ein:
-4 = 2 + b
Also
b = -6
Die Funktionsgleichung lautet also
y = x - 6
27.) Liegt der Punkt P(1,2) auf der Gerade g (A,B)? (Rechnerische Lösung!)
a.) A(9,17), B(17,5)
Geradengleichung aufstellen wie oben, dann den Punkt P in diese Geradengleichung einsetzen und sehen, ob sich eine wahre Aussage ergibt. Wenn ja, liegt P auf der Geraden, wenn nein, liegt er nicht auf der Geraden.
27.)
b.)
analog
Falls Rückfragen => Kommentar :-)
Besten Gruß