Differentialquotient berechnen. f(x)= 2x^3 - x^2- 5x + 1. Gesucht: Steigung in xo = -4

Question

Ich komme leider nicht weiter und verzweifle schön langsam.

Ich habe folgendes Beispiel: f(x)= 2x³ - x²- 5x + 1      Steigung in x_o = -4

Nun habe ich wie folgt gerechnet:

f´(-4)= (2(-4+h)³-(-4+h)²-5(-4+h)+1)-((-4)³-(-4)²-5(-4)+1)  =

                                                                                          h

  =-128+96h-24h²+2h³-16+8h-h²+21-5h+59 =-64 + 2h³-25h²+99h

                                 h                                                h

                              

Wie kann ich jetzt h herausheben , wenn ich die 64 habe.

Die Lösung ist aber  k=99

Bitte helft mir .

lg sabi

 

Answer 1

Da hast du dich wohl verrechnet. Die konstanten Glieder müssen sich zwangsläufig wegheben, weil sie in beiden Termen vorkommen.

Ich rechne mal von Anfang an:

$$ \frac { f ( - 4 + h ) - f ( - 4 ) } { h } = \frac { 2 · ( - 4 + h ) ^ { 3 } - ( - 4 + h ) ^ { 2 } - 5 · ( - 4 + h ) + 1 ) - \left( 2 ( - 4 ) ^ { 3 } - ( - 4 ) ^ { 2 } - 5 ( - 4 ) + 1 \right) } { h } \\ = \frac { 2 · \left( - 64 + 48 h - 12 h ^ { 2 } + h ^ { 3 } \right) - \left( 16 - 8 h + h ^ { 2 } \right) + 20 - 5 h + 1 + 128 + 16 - 20 - 1 } { h } \\ = \frac { - 128 - 16 + 20 + 1 + 128 + 16 - 20 - 1 + h · ( 96 + 8 - 5 ) + h ^ { 2 } · ( - 24 - 1 ) + h ^ { 3 } · 2 } { h } \\ = 99 + h · \left( - 25 h + 2 h ^ { 2 } \right) $$

Als Grafik:

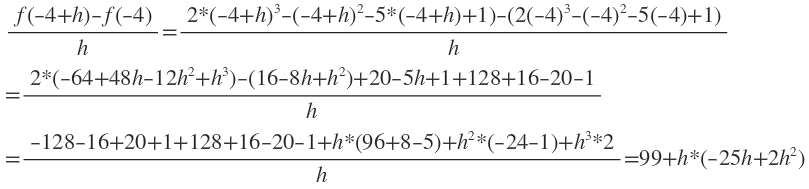
Im Grenzwert verschwinden jetzt die Terme, die noch h beinhalten und übrig bleibt

f'(-4) = 99

Ich habe auch gerade deinen Fehler gefunden: im Term, der aus f(-4) kommt hast du die 2 vor dem x³ vergessen.