Differenzierbarkeit reeller Funktion

Question

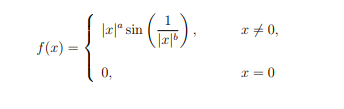
Text erkannt:

$f(x)=\left\{\begin{array}{ll}|x|^{a} \sin \left(\frac{1}{|x|^{b}}\right), & x \neq 0, \\ 0, & x=0\end{array}\right.$

Aufgabe: Seien a und b positive Zahlen und f: R -> R durch die Formel definiert. Zeige, dass f an allen von 0 verschiedenen Stellen differenzierbar ist.
Außerdem: Für welche Werte von a und b ist f auch bei 0 differenzierbar?
Wann ist f' stetig, unstetig und beschränkt oder nicht beschränkt?

Problem/Ansatz: Wie ist hier vorzugehen? Danke schonmal für jede potentielle Hilfe

Answer 1

Hallo

a) Zusammensetzung differenzierbarer Funktionen

b) 1. Stetigkeit bei 0 überprüfen, wenn stetig, dann GW des differenzenquotienten.

Gruß lul

Comments

Danke! Von Teil b) hätte ich nun zumindest eine grobe Vorstellung. Kannst du mir vielleicht noch einen Hinweis für den ersten Teil geben? Da weiß ich nicht wo anzufangen ist.

---

a) 1/x stetig für x≠0 sin(x) stetig, x^ a stetig deshalb auch Zusammensetzung und Produkt stetig.

lul