Aufgabe: Gleichungssystem aufstellen
Problem/Ansatz: Wie komme ich da auf die dritte Gleichung, die am Lösungsblatt steht?
Woher ist die 3??
Text erkannt:
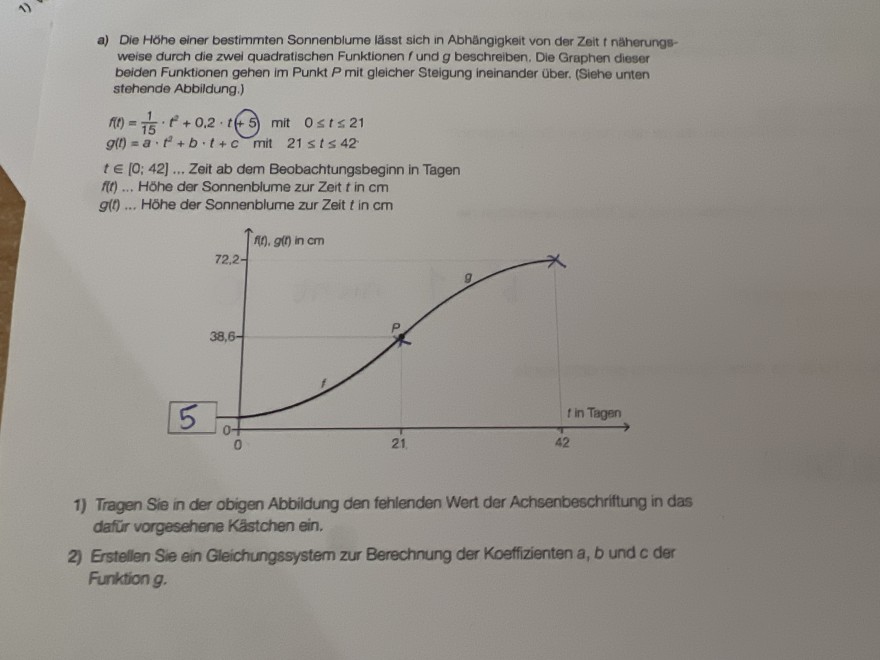
a) Die Hơhe einer bestimmten Sonnenblume lässt sich in Abhängigkeit von der Zeit t näherungsweise durch die zwei quadratischen Funktionen \( f \) und \( g \) beschreiben, Die Graphen dieser beiden Funktionen gehen im Punkt \( P \) mit gleicher Steigung ineinander über. (Siehe unten stehende Abbildung.)
\( f(t)=\frac{1}{15} \cdot t^{2}+0.2 \cdot t+5 \) mit \( 0 \leq t \leq 21 \)
\( g(t)=a \cdot t^{2}+b \cdot t+c \) mit \( 21 \leq t \leq 42 \)
\( t \in[0 ; 42] \)... Zeit ab dem Beobachtungsbeginn in Tagen
\( f(t) \)... Hohe der Sonnenblume zur Zeit \( t \) in \( \mathrm{cm} \)
\( g(t) \)... Hòhe der Sonnenblume zur Zeit \( t \) in cm
1) Tragen Sie in der obigen Abbildung den fehlenden Wert der Achsenbeschriftung in das dafur vorgesehene Kästchen ein.
2) Erstellen Sie ein Gleichungssystem zur Berechnung der Koeffizienten a, b und c der Furktion \( g \).

Text erkannt:
I: \( 21^{2} \cdot a+21 \cdot b+c=38,6 \)
II: \( 42^{2} \cdot a+42 \cdot b+c=72,2 \)
III: \( 42 \cdot a+b=3 \)