Berechnen Sie den vierten Tetraederpunkt T1

Question

Aufgabe:

Gegeben ist das Oktaeder mit den Eckpunkten P1 bis P6 mit P1 (6|3|10), P2 (12|3|4), P3 (6|9|4), P4 (0|3|4), P5 (6|-3|4) und P6 (6|3|-2).

b) Legen Sie ein Tetraeder gleicher Kantenlänge außen auf die Oktaederfläche P1, P3, P4 und ermitteln Sie den vierten Tetraederpunkt T1.
c) Verfahren Sie genauso mit der zu P, P3 P4 parallel verlaufenden Oktaederfläche und ermitteln Sie den Punkt des zweiten Tetraeders T2.

d) Berechnen Sie die Flächenwinkel (Winkel zwischen benachbarten Flächen) beim Oktaeder und beim Tetraeder.

Problem/Ansatz:

Ich versuche den ganzen Tag die Aufgabe zu lösen aber ich komme nicht weiter.

Ich weiß nicht wie ich entweder die Spitze T1 oder T2 berechnen soll, da Tetraeder nicht auf xy-Ebene liegt sondern schief im Raum.

Was ich bis jetzt berechnet habe:

die Seitenkante a (6√2 cm)

Körperhöhe des Tetraeders (4√3cm)

Mittelpunkt von dem Dreieck (P1, P3, P4) => S (4|5|6).

und mithilfe Geogebra herausgefunden, dass T1 bei (0|9|10) liegen soll und T2 bei (8|1|2) .

Was ich noch versucht habe:

Ebenegleichung:

E: x= (0|3|4) + s • (6|3|10) + t • (6|9|4)

und Normalvektor n = (-78|36|36) aber anscheinend ist er einfach n = (-1|1|1) ?

Geradengleichung:

g:x= (4|5|6) +  t • n

und dann Schnittpunkt Gerade Ebene und dadurch habe ich entweder r=0.01936 wenn n = (-78|36|36) oder

r = -0.3 wenn n = (-1|1|1)

aber iwie komme ich gar nicht auf die Lösung (0|9|10).

in der Skizze ist T1 als C dargestellt.

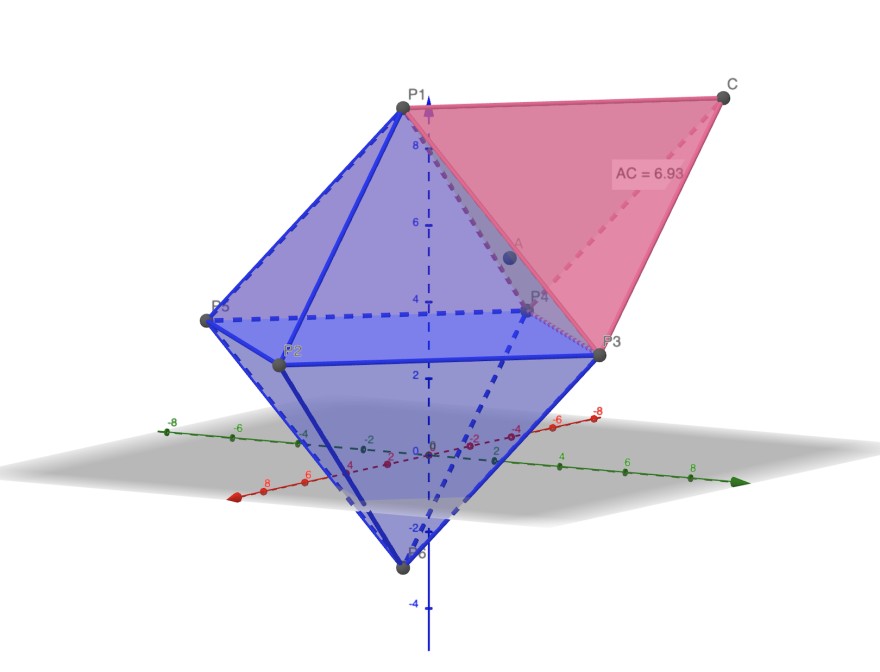
Ich wäre sehr dankbar wenn mir jemand helfen könnte, weil ich keine Ideen mehr habe, wie ich weiter vorgehen solle.

Answer 1

Gegeben ist das Oktaeder mit den Eckpunkten P1 bis P6 mit P1 (6|3|10), P2 (12|3|4), P3 (6|9|4), P4 (0|3|4), P5 (6|-3|4) und P6 (6|3|-2).

b) Legen Sie ein Tetraeder gleicher Kantenlänge außen auf die Oktaederfläche P1, P3, P4 und ermitteln Sie den vierten Tetraederpunkt T1.

Abstand² P1P3

[0, 6, -6]^2 = 72

T1 muss also zu P1, P3 und P4 auch einen Abstand von d^2 = 72 haben.

[x - 6, y - 3, z - 10]^2 = x^2 - 12·x + y^2 - 6·y + z^2 - 20·z + 145 = 72
[x - 6, y - 9, z - 4]^2 = x^2 - 12·x + y^2 - 18·y + z^2 - 8·z + 133 = 72
[x - 0, y - 3, z - 4]^2 = x^2 + y^2 - 6·y + z^2 - 8·z + 25 = 72

II - I ; III - I

- 12·y + 12·z - 12 = 0 --> y = z - 1
12·x + 12·z - 120 = 0 --> x = 10 - z

Wir setzen das nun in eine Gleichung ein

(10 - z)^2 + (z - 1)^2 - 6·(z - 1) + z^2 - 8·z + 25 = 72 --> z = 2 ∨ z = 10

Der Punkt außerhalb des Oktaeders ist der Punkt mit z = 10.

Daher sind die Koordinaten von T1

x = 10 - 10 = 0
y = 10 - 1 = 9
z = 10

Comments

Gegeben ist das Oktaeder mit den Eckpunkten P1 bis P6 mit P1 (6|3|10), P2 (12|3|4), P3 (6|9|4), P4 (0|3|4), P5 (6|-3|4) und P6 (6|3|-2).

Hier noch ein anderer Weg über die Höhe der Pyramide

P1P3 = [0, 6, -6]
P1P4 = [-6, 0, -6]

N = P1P3 x P1P4 = [-36, 36, 36] = -36·[-1, 1, 1]

Mittelpunkt der Seitenfläche P1P3P4

1/3·(P1 + P3 + P4) = [4, 5, 6]

Nun gehen wir vom Mittelpunkt über die Höhe zur Pyramidenspitze

T1 = [4, 5, 6] + 4·√3/√3·[-1, 1, 1] = [0, 9, 10]

---

Dankeschön !!

---

aber wie hast du [-36, 36, 36] ist P1P3 x P1P4 nicht [0, 0, 36] ?

und warum 4·√3 geteilt durch √3?

---

Danke für deine Antwort aber ich verstehe nicht warum T1 zu P1, P3 und P4 einen Abstand von d² und nicht einfach d haben muss?

---

aber wie hast du [-36, 36, 36] ist P1P3 x P1P4 nicht [0, 0, 36] ?

Du weißt vielleicht das das Kreuzprodukt zweier Vektoren senkrecht zu den multiplizierten Vektoren ist. [0, 0, 36] ist zu keinem der multiplizierten Vektoren Senkrecht also kann das doch nicht sein. Die Frage ist wie du auf so ein Ergebnis kommst. Rechne nochmals das Kreuzprodukt nach oder schau dir nochmals genau an wie man es rechnet.

und warum 4·√3 geteilt durch √3?

4·√3 ist die Länge der Höhe. Wir müssen den Vektor [-1, 1, 1] aber noch auf die Länge 1 normieren und damit durch √3 teilen.

---

Danke für deine Antwort aber ich verstehe nicht warum T1 zu P1, P3 und P4 einen Abstand von d2 und nicht einfach d haben muss?

Natürlich muss T1 einen Abstand von d haben. Ich vermeide aber gerne das Schreiben von Wurzeln und rechne daher immer nur mit dem quadrierten Abstand.

Das Skalarprodukt eines Vektors mit sich selbst bzw. das Quadrat eines Vektors, wenn wir das Quadrat mal als Skalarprodukt definieren, ist das Quadrat seiner Länge. Damit lässt es sich einfacher rechnen als, wenn man überflüssiger Weise noch die Wurzel zieht.

---

Danke noch mal! Hatte zuerst gedacht, dass das "x" bei dem Kreuzprodukt ein Malkreuz war und nicht gecheckt, dass √3 zu dem normierten Vektor gehört aber dann war zu spät mein Kommentar zu bearbeiten..

und die Frage mit dem d² war auch nicht so schlau.. bin einfach sehr müde und krank

aber danke, dass du dir Zeit nimmst und meine doofen Fragen beantwortest.

---

Kein Problem. Wichtig ist doch, dass du es im Endeffekt verstehst. Und wenn du es verstanden hast, dann gibt es keine doofen Fragen.

Ich erinnere mich an eine Schülerin, die 3 Wochen hintereinander Fragen zu Körpern und Dichten gestellt hat. Das ging darum, welche Kantenlänge z.B. ein Würfel haben muss, damit dieser Würfel aus purem Gold ein Gewicht von einem Kilogramm hat.

Ihr war das in der dritten Woche schon unangenehm zu fragen. Letztendlich hat sich die Fragerei aber gelohnt und sie hatte in der kommenden Klassenarbeit eine 2- gehabt.

---

Es gibt eine weit einfachere Art zum Punkt \(T_1\) zu gelangen. Man kann durch einfache elementargeometrsiche Überlegungen zeigen, dass \(T_1\) in der Ebene von \(P_1\), \(P_2\) und \(P_3\) liegen muss und \(P_1P_2P_eT_1\) bildet ein Parallelogramm. Daraus folgt dann$$T_1 - P_1 = P_3 - P_2 \\\begin{aligned} \implies T_1 &= P_3 - P_2 + P_1 \\&= \begin{pmatrix}6\\ 9\\ 4\end{pmatrix}-\begin{pmatrix}12\\ 3\\ 4\end{pmatrix}+\begin{pmatrix}6\\ 3\\ 10\end{pmatrix}=\begin{pmatrix}0\\ 9\\ 10\end{pmatrix}\end{aligned}$$Folgendes Bild zeigt das

(klick drauf!)

---

Danke, dass ergibt Sinn. Wäre nie auf die Idee gekommen. Manchmal denkt man zu kompliziert. :)

---

Wäre nie auf die Idee gekommen.

Du wärst sicher selbst drauf gekommen, wenn Du Dir z.B. selbst ein Modell aus Papier gebaut hättest. Jede Art von Visualisierung ist bei Aufgaben solcher Art sehr hilfreich.

---

Ich habe gerade zwei Modelle gebaut weil ich veranschaulichen muss, dass man mit Tetraedern und Oktaedern gleicher Kantenlänge den Raum lückenlos füllen kann und ja mit dem Modell ist das viel einfacher.

Answer 2

Hallo

1, finde die Ebene P1,P3,P4 möglichst Hesse Normalform

 2. finde die Mitte des Dreiecks. dann die Senkrechte  mit der berechneten Länge.

dein Normalenvektor wäre  richtig, falls die Parameterform der Ebene stimmte, stimmt aber nicht  besser (-1,1,1)  ist richtig

wenn die Skizze aus Geogebra stammt, kann das ja auch die Gleichung der Ebene angeben -x+y+z=7

Gruß lul

Comments

Hallo, danke für deine Antwort. Ich habe aber paar Fragen.

1. Was soll ich mit Hesse Normalform machen?

2. Was meinst du mit "die Senkrechte mit der berechneten Länge" ?

3. warum -x+y+z=7 ?