eine (von vielen!) weitere Lösung wäre noch die Beschreibung des Dreiecks auf Basis zweier Vektoren die durch die Seiten der Sechsecks definiert sind.
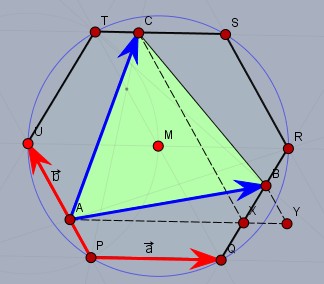
Die Seiten \(PQ\) und \(PU\) seien die Vektoren \(a\) und \(b\) (rot). Dann lassen sich die drei Punkte \(A\), \(B\) und \(C\) (auch bei einer beliebigen Teilung) durch Linearkombinationen von \(a\) und \(b\) darstellen. Ausgehend vom Punkt \(P\):$$A = \frac{1}{3}b\\ B= a + \frac{2}{3}(a+b)\quad\quad\quad |\, \vec{QR} = \vec{UT}=a+b\\ C=b + (a+b) + \frac{1}{3}a$$Die Fläche des Dreiecks ist dann schlicht das halbe Kreuzprodukt der beiden blauen Vektoren \(\vec{AB}\) und \(\vec{AC}\). \(F_6\) Ist die Fläche des Sechsecks und \(F_{\triangle}\) die des Dreiecks$$\begin{aligned} F_{\triangle} &= \frac{1}{2} \left( \vec{AB} \times \vec{AC} \right) \\ &= \frac{1}{2} \left( \left(\frac{5}{3}a + \frac{1}{3}b\right) \times \left(\frac{4}{3}a + \frac{5}{3}b\right) \right) \\ &= \frac{1}{2} \left( \frac{5}{3}a \times \frac{5}{3}b + \frac{1}{3}b \times \frac{4}{3}a \right) \\ &= \frac{1}{2} \left( \frac{25}{9}a \times b + \frac{4}{9}b \times a \right) \\ &= \frac{1}{2} \left( \frac{25}{9}a \times b - \frac{4}{9}a \times b \right) \\ &= \frac{7}{6}a \times b &&|\, a\times b= \frac{1}{3}F_6\\ &= \frac{7}{18} F_{6} \end{aligned}$$Allgemein gilt bei einer Teilung \(\tau =|AP|/|UP|\) der Seiten:$$F_{\triangle} = \frac{1}{2} (1-\tau + \tau^2)F_{6}$$Noch ein interessanter Aspekt in Sachen 'Goldener Schnitt': Wählt man \(\tau = \Phi\) bzw. \(\tau=-\Phi^{-1}\), so ist das Dreieck flächengleich zum Sechseck.