a)
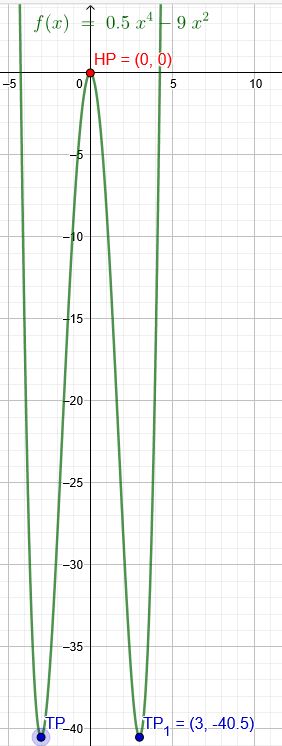
\(f(x)=0,5x^4-9x^2\)
\(f´(x)=2x^3-18x\)
\(2x^3-18x=0\)→ \(x^3-9x=0\)→ \(x*(x^2-9)=0\) → Satz vom Nullprodukt
\(x_1=0\) \(f(0)=0\)
\(f´´(x)=6x^2-18\) \(f´´(0)=-18<0 \) → Maximum
\(x_2=-3\) \(f´´(-3)=36 \) → Minimum
\(x_3=3\) \(f´´(-3)=36 \) → Minimum
b)
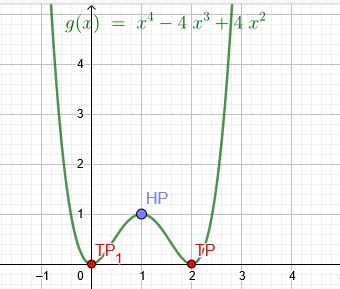
\(g(x)=x^4-4x^3+4x^2\)
\(g´(x)=4x^3-12x^2+8x\) → \(4x^3-12x^2+8x=0\)→ \(x^3-3x^2+2x=0\)→ Satz vom Nullprodukt
\(x_1=0\) \(g(0)=0\)
\(x^2-3x+2=0\) → \(x^2-3x=-2\)→ \((x-1,5)^2=-2+2,25=0,25 | \sqrt{x}\)
\(x-1,5=0,5\)
\(x_2=2\) \(g(2)=2^4-4*2^3+4*2^2=0\)
\(g´´(x)=12x^2-24x+8\) \(g´´(2)=12*2^2-24*2+8=8>0\) Minimum
\(x-1,5=-0,5\)
\(x_3=1\) \(g(1)=1^4-4*1^3+4*1^2=1\)
\(g´´(x)=12x^2-24x+8\) \(g´´(1)=12*1^2-24*1+8=-4<0\) Maximum
c)
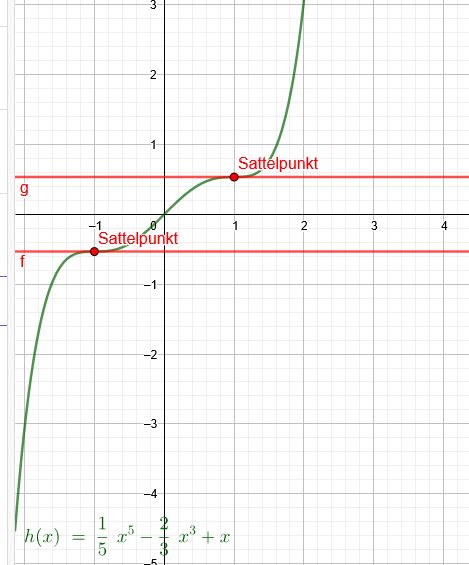
\(h(x)=\frac{1}{5}x^5-\frac{2}{3}x^3+x\)
\(h´(x)=x^4-2x^2+1\) \(x^4-2x^2+1=0\)
\(x^4-2x^2=-1\)
\((x^2-1)^2=-1+1=0 | \sqrt{}\)
\(x^2=1 \)
\(x_1=1\)
\(h´´(x)=4x^3-4*x\) \(h´´(1)=4*1^3-4*1=0\) hier liegt eine waagerechte Tangente vor , ist aber weder Hoch- noch Tiefpunkt.
\(h´´´(x)=12x^2-4\) \(h´´´(1)=12-4=8≠0\) Sattelpunkt
\(x_2=-1\)
\(h´´(x)=4x^3-4*x\) \(h´´(-1)=4*(-1)^3-4*(-1)=0\)hier liegt eine waagerechte Tangente vor , ist aber weder Hoch- noch Tiefpunkt.
\(h´´´(x)=12x^2-4\) \(h´´´(-1)=12-4=8≠0\) Sattelpunkt