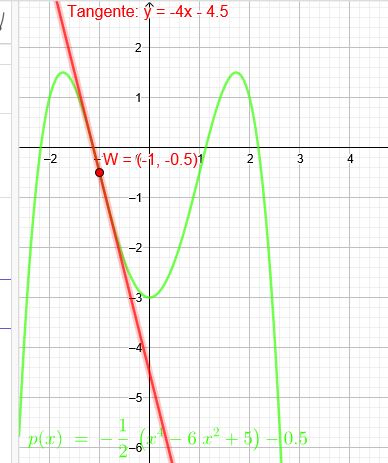
Der Graph einer ganzrationalen Funktion 4. Grades ist achsensymmetrisch zur y-Achse und hat im Wendepunkt W\((1|-\red{0,5})\) den Anstieg \(m=-4\).
Durch die Achsensymmetrie gilt auch W´\((-1|-0,5)\)
Ich verschiebe den Graphen um \(\red{0,5}\) nach \(\blue{↑}\):
Weiter mit der Nullstellenform der Parabel:
\(f(x)=a(x-1)(x+1)(x-N)(x+N)=a(x^2-1)(x^2-N^2)=a(x^4-N^2x^2-x^2+N^2)\)
\(f'(x)=a(4x^3-2N^2x-2x)\)
\(f''(x)=a(12x^2-2N^2-2)\)
Wendepunkteigenschaft: W´\((-1|...)\)
\(f''(-1)=a(12-2N^2-2)=0\)
\(a(10-2N^2)=0\)
\(N^2=5\)
Anstieg \(m=-4\) im Wendepunkt:
\(f'(x)=a(4x^3-12x)\)
\(f'(-1)=a(-4+12)=8a\)
\(8a=-4\)
\(a=-\frac{1}{2}\)
\(f(x)=-\frac{1}{2}(x^4-6x^2+5)\)
um \(\red{0,5}\) nach \(\blue{↓}\):
\(p(x)=-\frac{1}{2}(x^4-6x^2+5)-0,5\)