Bestimmen Sie jeweils den Betrag und das Argument der Zahlen

Question

Aufgabe:

Text erkannt:

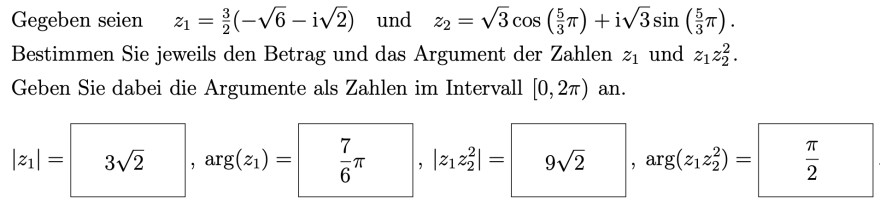
Gegeben seien \( \quad z_{1}=\frac{3}{2}(-\sqrt{6}-\mathrm{i} \sqrt{2}) \quad \) und \( \quad z_{2}=\sqrt{3} \cos \left(\frac{5}{3} \pi\right)+\mathrm{i} \sqrt{3} \sin \left(\frac{5}{3} \pi\right) \).
Bestimmen Sie jeweils den Betrag und das Argument der Zahlen \( z_{1} \) und \( z_{1} z_{2}^{2} \).
Geben Sie dabei die Argumente als Zahlen im Intervall \( [0,2 \pi) \) an.
\( \left|z_{1}\right|=3 \sqrt{2}, \arg \left(z_{1}\right)=\frac{7}{6} \pi,\left|z_{1} z_{2}^{2}\right|=9 \sqrt{2}, \arg \left(z_{1} z_{2}^{2}\right)=\frac{\pi}{2} \)

wie komme ich auf arg(z1z2^2) ? ich würde im Prinzip 7pi/6 mit 2x5pi/3 addieren, aber das ist falsch.

Answer 1

Passt doch. Es kommt dann \(\frac{9}{2}\pi\) raus. Wegen der \(2\pi\)-Periodizität ist aber \(\varphi_1=\varphi_2+k\cdot 2\pi\). In deinem Fall ist \(k=2\), also \(\varphi_2=\frac{1}{2}\pi\). Für gewöhnlich gibt man das Argument im Intervall \([0;2\pi]\) an.

Comments

Woher weiß ich welches k ich nehmen muss ?

---

Indem du es ausrechnest? Es sind doch einfach nur Vielfache von \(2\pi\). Wegen \(\frac{9}{2}\pi=4\pi + \frac{1}{2}\pi\).