Wie müssen a und b gewählt werden, damit f stetig ist?

Question

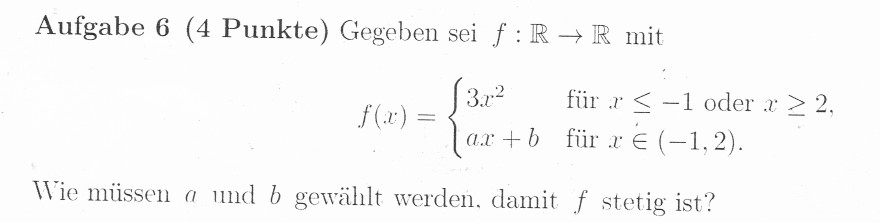
Text erkannt:

Aufgabe 6 (4 Punkte) Gegeben sei $f: \mathbb{R} \rightarrow \mathbb{R}$ mit
$f(x)=\left\{\begin{array}{ll} 3 x^{2} & \text { für } x \leq-1 \text { oder } x \geq 2, \\ a x+b & \text { für } x \in(-1,2) . \end{array}\right.$

Wie müssen $a$ und $b$ gewählt werden, damit $f$ stetig ist?

Answer 1

Dann muss gelten a*(-1)+b = 3    und  a*2+b = 12.

Damit kannst du ja a und b ausrechnen.

Comments

Kommt bei a=3 und b=6 oder a=-9 und b=-6 raus ?

---

-a+b = 3

-2a+b = 12

subtrahieren:

a= -9

einsetzen:

-(-9)+b= 3

b= -6

---

Du solltest m nicht kritiklos kopieren.

---

Wieso eigentlich (-2)a....

---

Weil m. das so schrieb, dem ich vertraute, ohne weiter hinzuschauen.

Komisch war nur die Schreibweise ohne Klammer. Bei ihm hat wohl das Minus von -1 abgefärbt.

Korrektur:

-a+b = 3
2a+b = 12

---------.

-3a = -9

a= 3

b= 6

---

stimmt. Das "minus" passt nicht. Das Intervallende

war ja bei 2. Das korrigiere ich.

---

Ist meine Theorie richtig, dass du das MINUS von -1 unterbewusst übernommen hast?