Vektorraum axiome zeigen?

Question

Aufgabe:

Sei \( V:=\{(a, b): a, b \in \mathbb{R}\} \). Ferner seien in \( V \) eine innere Verknüpfung + und eine äußere Verknüpfung \( \cdot \) folgendermaßen definiert:
\( (a, b)+(c, d)=(a+c, b+d) \quad \alpha \cdot(a, b)=(\alpha a, 0) \quad \alpha \in \mathbb{R} \)

Man zeige, dass alle Eigenschaften eines \( V R \) erfüllt sind bis auf die Bedingung \( 1 \cdot \boldsymbol{a}=\boldsymbol{a} \) (d.h.diese Bedingung folgt nicht aus den anderen Vektorraum-Axiomen).

Problem/Ansatz:

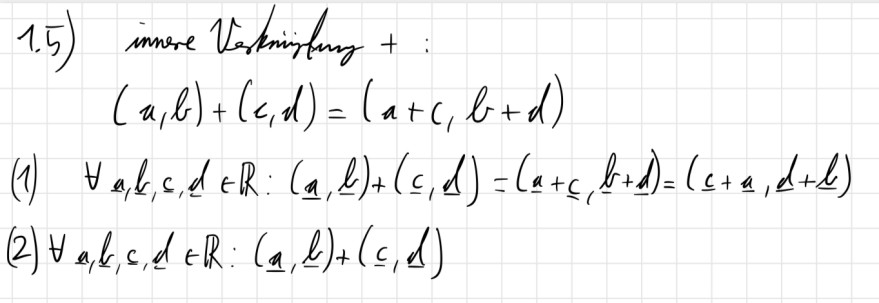
Ich komme hier nicht weiter...

Answer 1

Hallo

was du mit 1 zeigen willst sehe ich nicht,  bei 2 zeigst du, dass die Summe von 2 Vektoren wieder in V liegt,  da a+c und b+d in R

es fehlt r*(a,b) liegt in V das gilt auch da (ra,0) in V liegt, bleibt nur zu zeigen dass 1*(a,b)≠(a,b ist falls b≠0

lul