In Dubai werden im Meer künstliche Inseln aufgeschüttet. Die Küsten einer Insel werden (wie abgebildet) durch die Funktionen f (Strand) und g (Wohnen) beschrieben. (1 LE = 100 m)
\( f(x)= -\frac{1}{8}x²+x \)
\( g(x)= (2x-20) * e^{x-10/5} \)
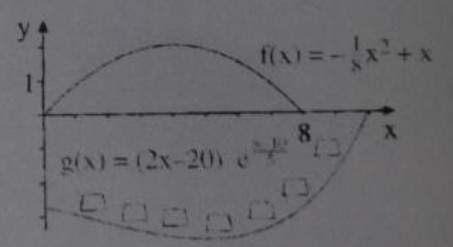
a) Zeigen Sie, dass \( G(x)=(10 x-150) \cdot e^{\frac{x-10}{5}} \) eine Stammfunktion von G ist. Berechnen Sie den Flächeninhalt der Insel.
b) Welche maximale Nord-Süd-Ausdehnung hat der untere Teil der Insel, d.h. das Wohngebiet?