Ursprungsgeraden bilden mit Wert t

Question

Eine Ursprungsgerade durch B(2t/2t²) und eine Gerade g durch B mit m = -3t² bilden mit der x-Achse ein Dreieck. Für welche Wahl von t ist das Dreieck rechtwinklig?

 

zuerst habe ich m von der U.gerade ausgerechnet

2t² = m * 2t     l /2t

t  = m

dann b von der normalen g

2t² = -3t³ * 2t + b

2t² + 6t³ = b

 

wie stimme ich jetzt t ein dass es ein rechtwinkliges dreieck mit der x achse bildet?

Answer 1

Die Steigung der einen Geraden ist t.

Ihre Gleichung y = tx 

Die Steigung der andern -3t²

Wenn die beiden senkrecht aufeinander stehen sollen, muss das Produkt ihrer Steigungen  -1 sein.

Also t * (-3t²) = - 1

-3t³ = -1

t³ = 1/3

t = (1/3)^{1/3}

Damit kommst du nun wohl selbst zum Ergebnis.

Comments

vielen dank, jetzt ist mir alles kalr einfach auf orthogonalitär prüfen

Answer 2

m₁ = t

für die Ursprungsgerade hast Du richtig ausgerechnet. Für die Gerade G war

m₂ = -3t^2

gegeben. Damit ein rechter Winkel entsteht muss gelten:

m₁ * m₂ = -1

t * -3t^2 = -1
t^3 = 1/3
t = 3.Wurzel(1/3) = 0,6934

Wir zeichnen das ganze mal

 

Answer 3

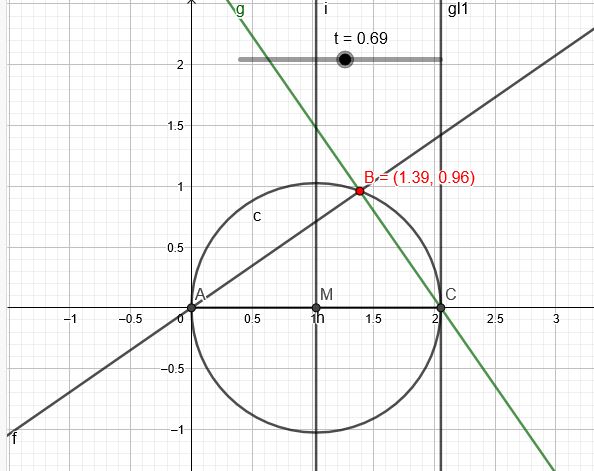
Eine Ursprungsgerade durch \(B(2t|2t^2)\) und eine Gerade g durch B mit \(m=-3t^2\) bilden mit der x-Achse ein Dreieck. Für welche Wahl von \(t\) ist das Dreieck rechtwinklig?

Zugang über den Thaleskreis:

Ursprungsgerade durch \(B\):

\( \frac{y-2t^2}{x-2t}=t\)   →  \( y=t*x\)

Gerade g durch B:

\( \frac{y-2t^2}{x-2t}=-3t^2\) →  \( y=-3t^2*x+6t^3+2t^2\)

Nullstelle dieser Geraden:

\( -3t^2*x+6t^3+2t^2=0 |:(-3t^2)\)

\(x=2t+\frac{2}{3}\)   →  \(N(2t+\frac{2}{3}|0)\)

Thaleskreis über Strecke Urprung bis N mit Mittelpunkt \(M(t+\frac{1}{3}|0)\)

\((x-(t+\frac{1}{3}))^2+y^2=(t+\frac{1}{3})^2\)

\(B(2t|2t^2)\) soll auf diesem Kreis liegen:

\((2t-(t+\frac{1}{3}))^2+4t^4=(t+\frac{1}{3})^2\)

\((t-\frac{1}{3})^2+4t^4=(t+\frac{1}{3})^2\)

\(t^2-\frac{2}{3}*t+\frac{1}{9}+4t^4=t^2+\frac{2}{3}*t+\frac{1}{9}\)

\(t^4-\frac{1}{3}*t=0\)

\(t*(t^3-\frac{1}{3})=0\)

\(t_1=0\)

\(t^3=\frac{1}{3}\)

\(t=\frac{1}{\sqrt[3]{3}}≈0,693\)