Berechnen Sie die Abmessungen a, b und h der Pyramide so, dass daraus ein grösstmögliches Pyramidenvolumen entsteht.

Question

Aufgabe:

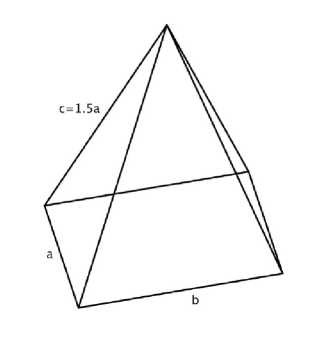
Es soll ein Rohrgerüst in Form einer geraden Pyramide mit rechteckiger Grundfläche gemäss Skizze hergestellt werden.
Dazu stehen total 60 Meter Stahlrohr zur Verfügung.
Berechnen Sie die Abmessungen a, b und h der Pyramide so, dass daraus ein grösstmögliches Pyramidenvolumen entsteht.
Die Dicke der Rohre kann vernachlässigt werden.
Die Pyramide besteht aus je zwei Rohren der Länge a und b sowie aus vier Rohren der Länge c, wobei c = 1.5.a gilt.

Problem/Ansatz:

Extremwertaufgabe: Wobei helfen mir "total 60 Meter Stahlrohr zur Verfügung"? Es ist mir klar, dass die Zielfunktion Volumen der Pyramide sei und später die Ableitung davon machen muss, aber die Nebenbedingungen sind für mich verwirrend ...

Besten Dank für Ihre Hilfe im Voraus

Comments

Du bist nun seit 6 Jahren dabei und hast bald 100 Fragen gestellt. Meinst Du es ist möglich auch mal einen Kommentar mit "Danke" oder "Habs verstanden" zu hinterlassen? Ein Daumen oder Stern würde alternativ auch gelten.

Es arbeiten hier Menschen (nein, keine KI), und eine Rückmeldung jedweder Art würde diesen gut tun. Das sollte der Mindestlohn sein ;).

Answer 1

Die Pyramide besteht aus je zwei Rohren der Länge a und b sowie aus vier Rohren der Länge c, wobei c = 1.5.a gilt.

Alle diese Rohrlängen zusammen müssen 60 Meter ergeben. Damit kannst du also die Nebenbedingung aufstellen.

Answer 2

Nebenbedingungen

L = 2·a + 2·b + 4·1.5·a = 60

(a/2)^2 + (b/2)^2 + h^2 = (1.5·a)^2

Hauptbedingung

V = 1/3·G·h

Ich erhalte zum Vergleich

a ≈ 5.665 m
b ≈ 7.342 m
h ≈ 7.120 m