Text erkannt:
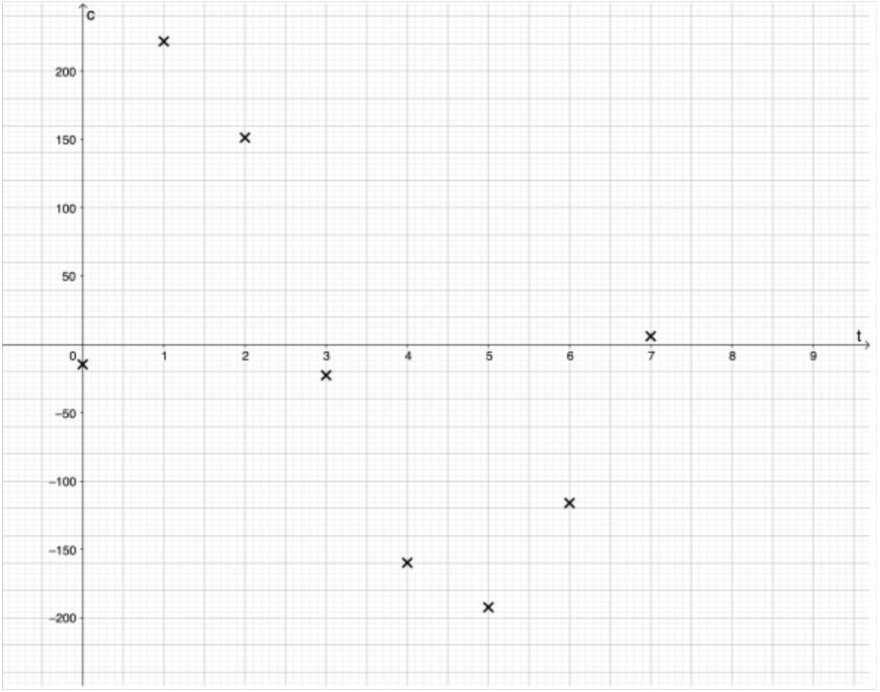
(a) Wir betrachten die Funktion \( c(t) \), welche die Netto-Ausschüttungsrate (d. h. mit Berücksichtigung des Abbaus) des Hormons Kortisol in \( \left[\frac{\mathrm{nmol}}{\ell \cdot \mathrm{s}}\right] \) der Hypophyse nach \( t \) Stunden angibt. Gegeben ist folgende Wertetabelle sowie der zugehörige Graph.
\begin{tabular}{|c||c|c|c|c|c|c|c|c|}
\hline\( t \) & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\
\hline\( c(t) \) & \( -14,6 \) & 221,7 & 151,3 & \( -22,6 \) & \( -159,7 \) & \( -192,3 \) & \( -116,0 \) & 6,0 \\
\hline
\end{tabular}
(i) Was stellt im Sachzusammenhang das Integral \( \int \limits_{0}^{5} c(t) d t \) dieser Funktion dar?
(ii) Berechnen Sie näherungsweise die Netto-Ausschüttung des Kortisols für \( t \in[1 ; 6] \) und damit die durchschnittliche Netto-Ausschüttung pro Stunde in diesem Zeitraum. Hinweis: Es soll zum Zeitpunkt \( t=1 \) gestartet werden, nicht „in der ersten Stunde"!
(iii) Erstellen Sie ein Streudiagramm und veranschaulichen Sie die Ergebnisse aus (ii) aus im Graphen.