Aufgabe: Momentane Änderungsrate gleich mit mittlerer Änderungsrate
Problem/Ansatz:
!Dieses Bild ist NICHT aus einem Buch!
Aufgabenstellung (Graph ist unten zu sehen)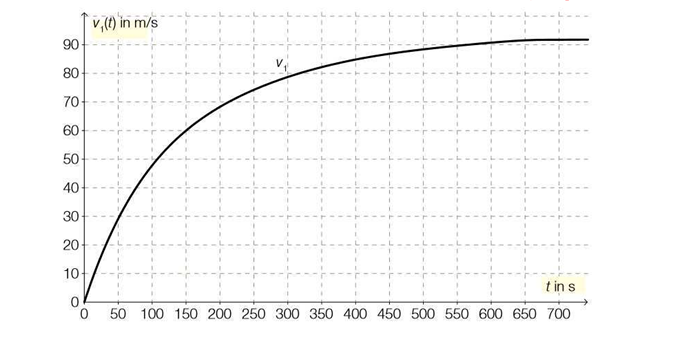 :
:
a) Die Daten eines Beschleunigungstests vom Stillstand bis zur Höchstgeschwindigkeit (die Geschwindigkeit \( v_{1}(t) \) ist in Metern pro Sekunde und die Zeit \( t \) in Sekunden angegeben) sind im nachstehenden Zeit-Geschwindigkeit-Diagramm näherungsweise dargestellt.
1) Bestimme die mittlere Änderungsrate der Geschwindigkeit im Zeitintervall \( [0 \mathrm{~s} ; 700 \mathrm{~s}] \) und gib einen Zeitpunkt an, zu dem die momentane Änderungsrate der Geschwindigkeit größer ist als die ermittelte mittlere Änderungsrate.
Die mittlere Änderungsrate habe ich bereits ausgerechnet: 0,13m/ss
Ich verstehe nur nicht, wie man das ablesen soll.