Eine Stammfunktion könnte man folgendermaßen finden:
\(f(x)=|x|\cdot |x-1|=\begin{cases} x\cdot (x-1) &, x\leq 0 \\ -x\cdot (x-1) &,0< x \leq 1 \\ x\cdot (x-1) & ,1< x \end{cases} = \begin{cases} x^2-x &, x\leq 0 \\ -x^2+x &,0< x \leq 1 \\ x^2-x & ,1< x \end{cases}\)
D.h.
\(F(x)=c+\begin{cases} \frac{1}{3}x^3-\frac{1}{2}x^2 &, x\leq 0 \\ -\frac{1}{3}x^3+\frac{1}{2}x^2 &,0< x \leq 1 \\ \frac{1}{3}x^3-\frac{1}{2}x^2 & ,1< x \end{cases}\)
Jetzt ist nur noch das Problem, dass F bei 1 nicht stetig ist. F muss aber sogar differenzierbar sein. Deswegen verschieben wir den letzten Teil nach oben (die Ableitung bleibt ja dann dieselbe):
\(F(x)=c+\begin{cases} \frac{1}{3}x^3-\frac{1}{2}x^2 &, x\leq 0 \\ -\frac{1}{3}x^3+\frac{1}{2}x^2 &,0< x \leq 1 \\ \frac{1}{3}x^3-\frac{1}{2}x^2+\frac{1}{3} & ,1< x \end{cases}\).
Diese Funktion ist überall differenzierbar, und wenn man sie ableitet, erhält man f (das ist ja eigentlich klar, außer an den Stellen 0 und 1, da müsste man die Ableitung nochmal per Hand mithilfe des Differentialquotienten überprüfen, ob da wirklich f(0) bzw. f(1) rauskommen).
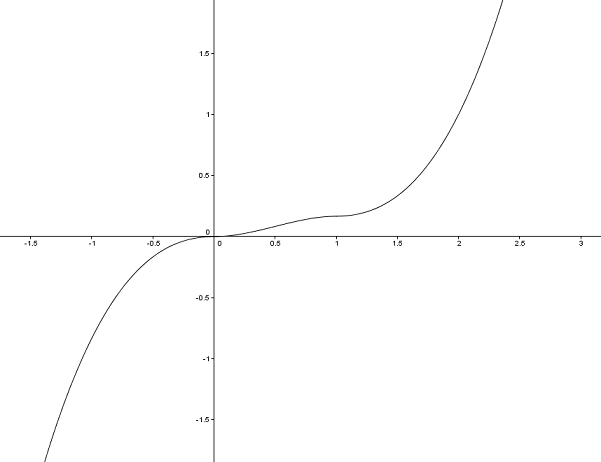
Und so sieht die Stammfunktion aus (hier ist c=0):