Hi Emre,
a)
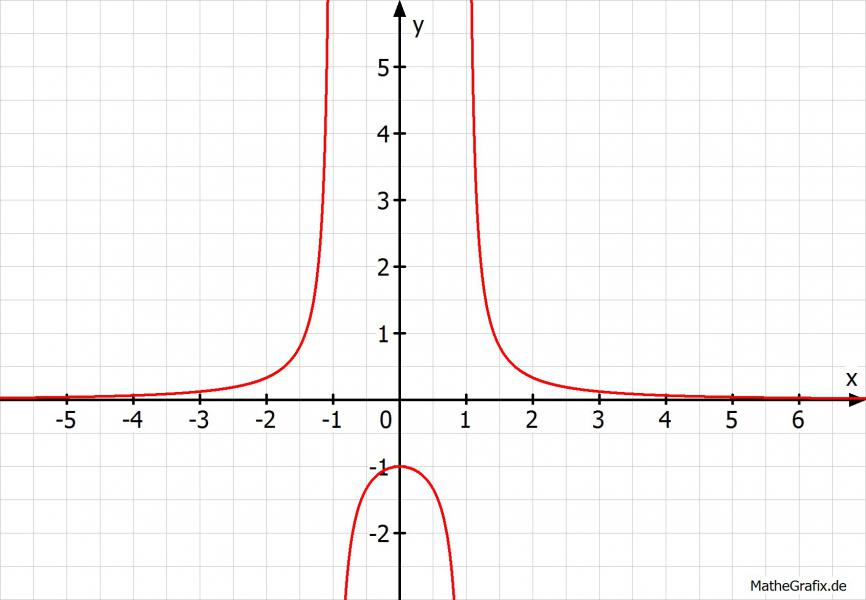
f(x) = 1/(x^2-1)
Nullstellen:
Gibt keine, da der Zähler nie 0 wird (und nur der ist von Belang)
Symmetrie:
Achsensymmetrie f(x) = f(-x)
Polstelle:
Was Du meinst scheint mir eine (hebbare) Definitionslücke zu sein. Also wenn man eine Kurve hat und diese ein "Loch" hat. Und man dieses kenntlich macht. Eine Polstelle ist aber was anderes. Das ist eine senkrechte Asymptote, also der Graphen geht hier gegen Unendlich.
Das ist immer für Nennernullstellen der Fall, die es nicht im Zähler gibt (diese wären dann eventuell hebbar).
x = -1 und x = 1 sind unsere Polstellen
Asymptote:
Die senkrechten habe ich schon genannte. Die waagerechte Asymptote -> hier wird das Verhalten von x gegen + und - unendlich angeschaut. Hier kann man auch Argumentieren "Der Zählergrad ist kleiner als der Nennergrad" (also auf die höchste Potenz bezogen) und um es unmathematisch auszudrücken "Der Nenner wächst schneller als der Zähler" und deswegen geht das ganze gegen 0.
y = 0
b)
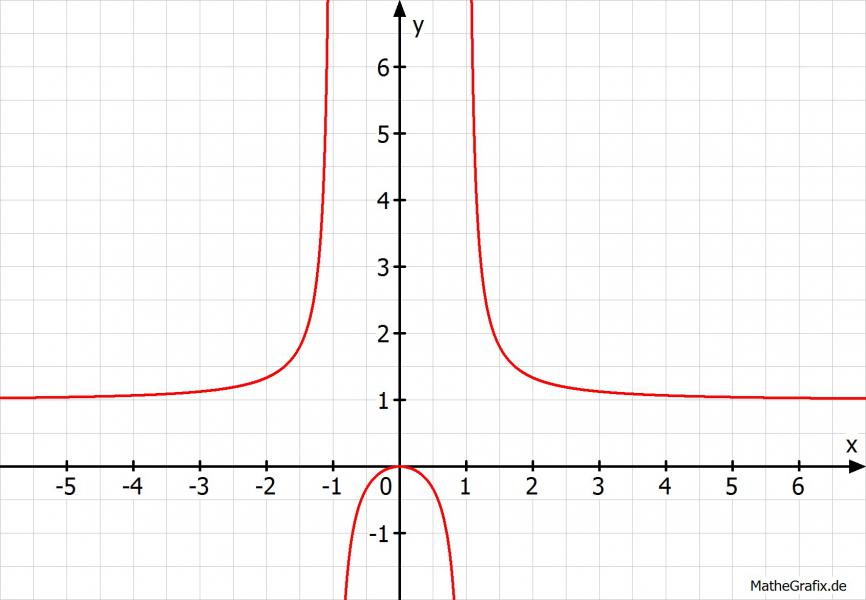
x^2/(x^2-1)
Nullstellen:
Diese ist hier 0, denn x^2 = 0 --> x = 0
Symmetrie:
Achsensymmetrie f(x) = f(-x)
Polstelle:
Auch hier sind unsere Nennernullstellen von Relevanz. Es sind dieselben.
x = -1 und x = 1 sind unsere Polstellen
Asymptote:
Die senkrechten habe ich schon genannte. Die waagerechte Asymptote ist hier über "Zählergrad gleich Nennergrad", also die Vorfaktoren der jeweils höchsten Potenz sind anzuschauen und das ist ja jeweils 1 und damit
--> y = 1
Hoffe Du kommst damit weiter ;),
Grüße