Parameter bestimmen, damit das Integral bestimmen Wert erreicht.

Question

Bestimmen Sie den gesuchten Parameter a der Funktion \( f(x) \), wenn gelten soll:

\( \int \limits_{-15}^{13} a x^{4}-2 x^{2}+4 d x=147495 \)

Answer 1

Hallo immai,

 

hinter dem Integralzeichen steht die zu integrierende Funktion

f(x) = ax⁴ - 2x² + 4

Zum Integrieren brauchen wir ja immer eine Stammfunktion, eine solche wäre hier:

F(x) = a/5 * x⁵ - 2/3 * x³ + 4x

Hauptsatz der Integralrechnung (etwas salopp): Stammfunktion obere Grenze minus Stammfunktion untere Grenze = Integral

Also

a/5 * 759375 - 2/3 * 3375 + 4 * 15 -

(a/5 * (-759375) - 2/3 * (-3375) + 4 * (-15))

=

303750a - 4/3 * 3375 +120

=

303750a - 4380 = 147495 | + 4380

303750a = 151875 | : 303750

a = 0,5

 

"Probe":

www.integralrechner.de

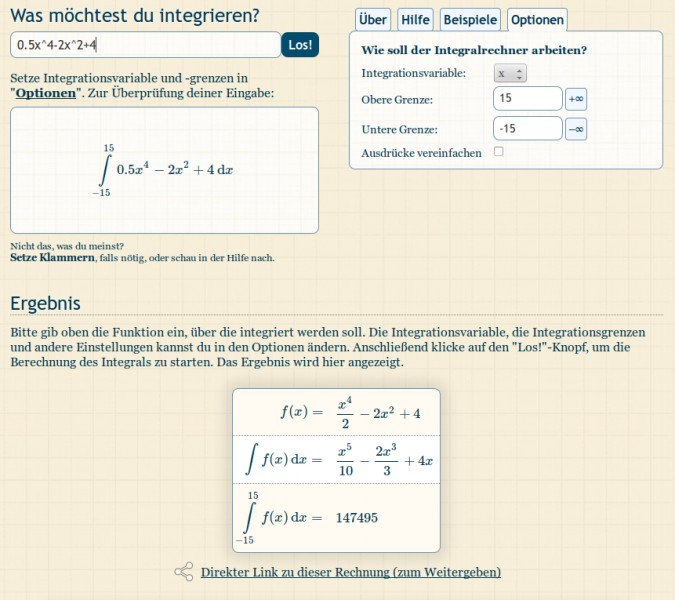
Besten Gruß

Comments

Ok danke ich selbst haber aber -0.47 rausbekommen. Macht man eigentlich immer uuerst die oberre dann min7s die untere beim interhral zeichen?? Ich hab zuerst die unter dann minus die obere gmecaht?

---

Gern :-)

Ja, oben an das Integralzeichen kommt die obere Grenze, unten die untere Grenze; und dann F(oben) minus F(unten).

Du hast es umgekehrt gemacht und deshalb auch -0,47 statt des richtigen Ergebnisses +0,5.