Der Graph der Funktion gibt Aufschluss zu ein paar Eigenschaften der Funktion.
Er hat bei x= -2 einen Pol, bei x=-1 einen Knick (das ist keine Unstetigkeitsstelle (erst die Ableitung wäre an der Stelle x=-1 unstetig)) und bei x=2 eine Sprungstelle.
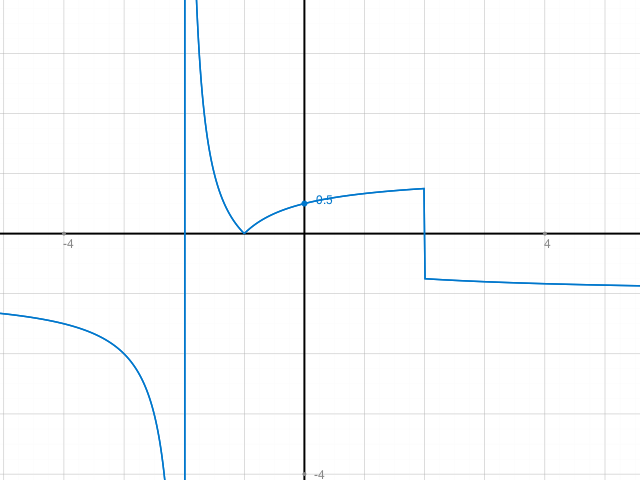
Nun sollst du das aber berechnen, nicht nur zeichnen.
Als Erstes kannst du den Nenner 4 -x^2 betrachten.
In dessen Nullstellen ist der Wert der Funktion nicht definiert.
4 - x^2 = (2+x)(2-x) = 0
Kandidaten für eine Unstetigkeitsstelle sind x = - 2 und x = 2.
Nun faktorisiere ich noch den Zähler: |x^2 -x -2| = |(x-2)(x+1)|
Man sieht, dass sich beim Bruch (x-2) rauskürzen liesse, während (x+2) auf jeden Fall im Nenner bleibt.
Daher:
Fall x = - 2. Die Funktion hat einen Pol in x = -2.
Fall x=2 genauer untersuchen:
Fall x > 2 (beliebig nahe bei 2): x-2 > 0 und x+1 > 0. Man kann die Betragstriche im Zähler einfach weglassen.
f(x) = |(x-2)(x+1)| / ((x-2) (x+2))
= ((x-2)(x+1))/((x-2)(x+2)) kürzen
= (x+1)/(x+2) Definitionslücke ist weg. Man kann Werte beliebig nahe rechts von 2 einsetzen.
und kommt im Grenzfall auf +3/4
Fall -1< x < 2 (beliebig nahe bei 2): x-2 > 0 und x+1 > 0. Man kann die Betragstriche im Zähler weglassen, wenn man ein (x-2) durch -(x-2) ersetzt.
f(x) = |(x-2)(x+1)| / ((x-2) (x+2))
= (-(x-2)(x+1))/((x-2)(x+2)) kürzen
= -(x+1)/(x+2) Definitionslücke ist weg. Man kann Werte beliebig nahe rechts von 2 einsetzen.
und kommt im Grenzfall auf -3/4
Fazit: An der Stelle x=2 springt die Funktion von -3/4 nach 3/4. Man hat dort eine Sprungstelle.