Monotonieverhalten untersuchen Funktion f(x) = x^4 · e^{-x/3}

Question

Ich habe folgende Funktion gegeben und soll sie auf Monotonie untersuchen.

Ich habe die erste Ableitung gebildet und geschaut wo sie postivi oder negativ ist.

Reicht das schon aus oder ist es besser die zweite Ableitung noch zu bilden und ermitteln ob es ein Hoch- oder Tiefpunkt ist?! Nachdem ich die gebildet habe und die Nullstellen von der 1. Ableitung eingesetzt habe kam 0 heraus. Das verwirrt ein wenig.

Vielen dank schonmal für die Hilfe.

$$ \left. \begin{array} { l } { f ( x ) = x ^ { 4 } · e ^ { - \frac { x } { 3 } } } \\ { f ^ { \prime } ( x ) = e ^ { - \frac { x } { 3 } } · \left( 4 x ^ { 3 } - \frac { x ^ { 4 } } { 3 } \right) } \\ { f ^ { \prime \prime } ( x ) = e ^ { - \frac { x } { 3 } } \left( \frac { 1 } { 9 } x ^ { 4 } - \frac { 8 } { 3 } x ^ { 3 } - 12 x ^ { 2 } \right) } \end{array} \right. $$

Answer 1

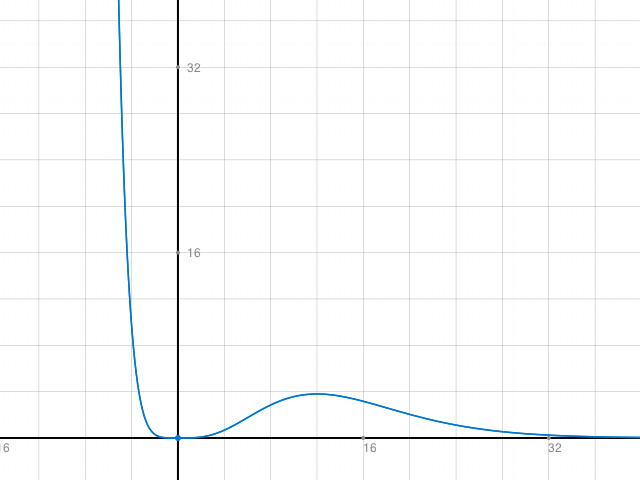
Ich habe hier nicht f(x) sondern f(x)/100 eingezeichnet, damit man neben dem relativen Minimum auch das relative Maximum sieht.

Die Fallunterscheidung positiv / negativ genügt eigentlich.

f ' (x) = 0 heisst

4x^3 - x^4/3 = 0 

12 x^3 - x^4 = 0

x^3 (12 -x) = 0            x1=0 ist dreifache Nullstelle: Vorzeichenwechsel!

                                      x2=12 einfache Nullstelle: Vorzeichenwechsel!

Vorzeichenwechsel in der Ableitung heisst Max oder Min. Wenn die zweite Ableitung auch 0 ist, muss man anders testen, ob die Kurve links oder rechts der NS fällt oder steigt.

Anmerkung: Man hat Vorzeichenwechsel bei NS von Polynomen, wenn die Vielfachheit der Nullstelle ungerade ist.