Welche Seite hast Du zugemacht?
Es ist egal was Du als Stüztvektor oder Richtungsvektor nimmst.
Stützvektor bedeutet ja nur so viel "Wie komme ich vom Ursprung überhaupt erstmal auf die Gerade" (da einfach den Ortsvektor eines aufliegenden Punktes nehmen. Es bietet sich hier C an, da dieser ohne b gegeben ist).
Den Richtungsvektor kann man dann so übersetzen -> Wie komme ich nun von diesem Aufpunkt (also bei uns C) weiter? So weiter, dass ich auf meiner Geraden bin.
Das würde ich zeichnerisch eventuell wie folgt erklären wollen:
(Damit es übersichtlicher ist nur 2D. Verzeih meine "künsterlische" Ader, bin halt doch mehr Mathematiker :P...solange man es erkennen kann^^)
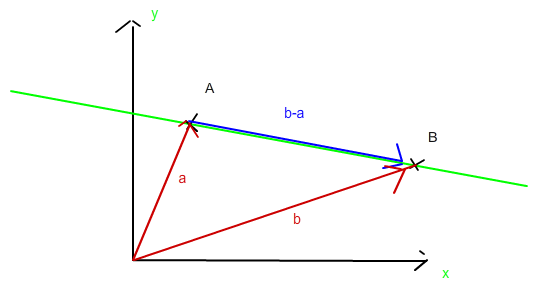
Also Du nimmst den Ortsvektor a um auf die grüne Gerade zu kommen. Und nun willst Du auf der grünen Geraden jeden Punkt erreichen. Dafür brauchst Du s*(b-a), also s als Vorfaktor um die Länge zu bestimmen und der Zweck von (b-a) ist ja aus dem Bild zu entnehmen.
Dass es genau b-a sein muss (oder andersrum) siehst Du so -> Du möchtest den blauen Pfeil durch bereits bekannte Vektoren (also a und b) beschreiben. Deshalb gehst Du vom Pfeilanfang zum Nullpunkt (-a) und von dort aus zur Pfeilspitze (+b). Es entsteht -a+b = b-a -> Der Richtungsvektor.
Du hast also damit Deine Gerade beschrieben. Durch den Ortsvektor kommst Du auf die Gerade und mit dem Richtungsvektor erreichst Du dann letztlich alle Punkte auf der Geraden.
(Ups, etwas viel geworden, aber hoffentlich nicht zu viel^^)