Bestimmung der Monotonie und der Extrema von f : R → R mit f(x)= x3*exp(1−(x2/6))

Question

Untersuchen Sie die Funktion f : R → R mit
f(x)= x³*exp(1−(x²/6))
auf Monotonie und bestimmen Sie alle lokalen Extrema. Bestimmen Sie auch die exakten Funktionswerte in den lokalen Extremstellen und in den Punkten mit horizontaler Tangente.

Präzisision: EDIT: f(x)= x³*exp(1−(x²/6)) = x³ e^1-(x2/6)

Comments

f(x)= x^3*exp(1−(x^2/6))


meinte ich.

Answer 1

f(x) = x³·e^{1 - x^2/6}

f'(x) = 1/3·e^{1 - x^2/6}·(9·x² - x⁴)

Symmetrie

Punktsymmetrie zum Ursprung

Verhalten im Unendlichen

lim (x → ±∞) = 0

Extrempunkte f'(x) = 0

9·x² - x⁴ = 0

x = -3 ∨ x = 3 ∨ x = 0

f(-3) = - 27·e^{- 1/2} = -16.38 --> TP

f(0) = 0 --> SP

f(3) = 27·e^{- 1/2} = 16.38 --> HP

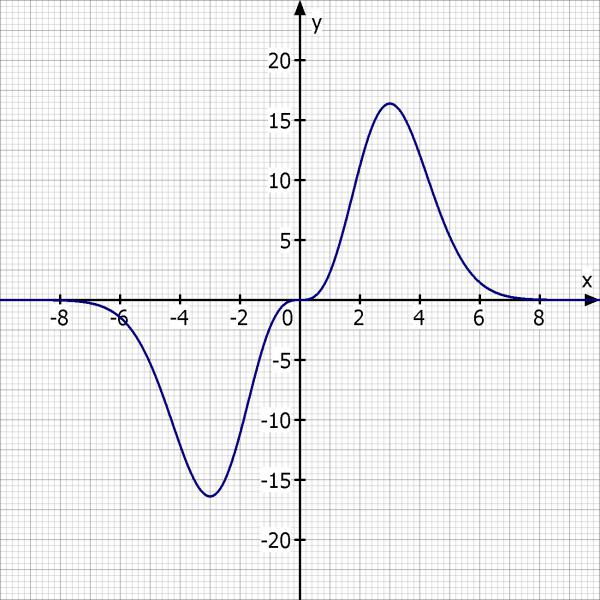
Skizze