f'(x)=-2(-e^2x)+2e^x
-2(-e^2x)+2e^x = 0
2e^x = - 2e^{2x}
Da e^x und e^2x nie 0 ist, geht das nicht.
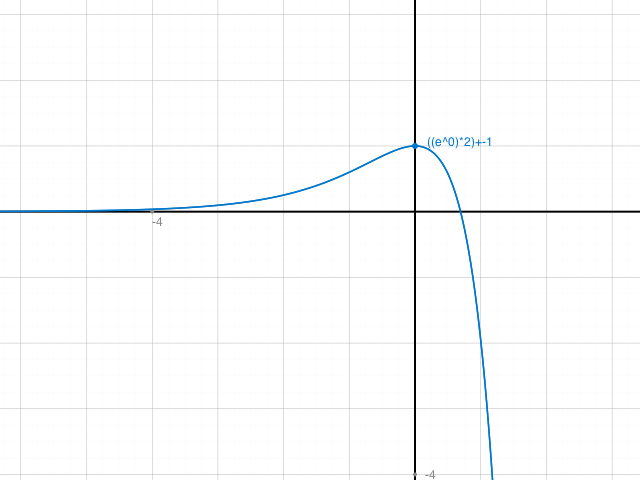
Ich betrachte (unten mal den Graphen von f(x)=-e^{2x} + 2e^x
und sehe, dass du falsch abgeleitet hast.
f'(x)=2*(-e^{2x})+2e^x = -2e^{2x} + 2e^x = 0
2 e^{2x} = 2 e^x |:2 e^x (nach Potenzgesetzen)
e^x = 1 |ln links und rechts
x = ln(1) = 0 Also x=0 ist Extremalstelle.
Wenn du die Vorzeichen korrigierst, kannst du bestimmt auch die andern Gleichungen lösen. Oder