Gemäss Mengenschreibweise in der Fragestellung sind hier wohl auch Umkehrzuordnungen (nicht unbedingt Funktionen zu betrachten)
Gegeben seien folgende Funktionen
g1 : { ℕ→Ζ ; x→x} g2: {{ M ⊂ ℕ : M endlich} → ℕ ; M → |M|} g3:{R→R; x→x4} g4: {ℚ→R; x → √(2)}
Bestimme:
Z1:= g1-1(Z\{1})
Z2:=g2-1({0})
Z3:=g3-1((-∞ , 0))
Z4=g4-1([-2,2])
Z1, Z2… sind Teilmengen der Grundmenge. Sie bestehen aus allen Elementen, die ein Bild im angegebenen Bereich enthalten.
Du willst ja nur wissen, WIE man die bestimmt.
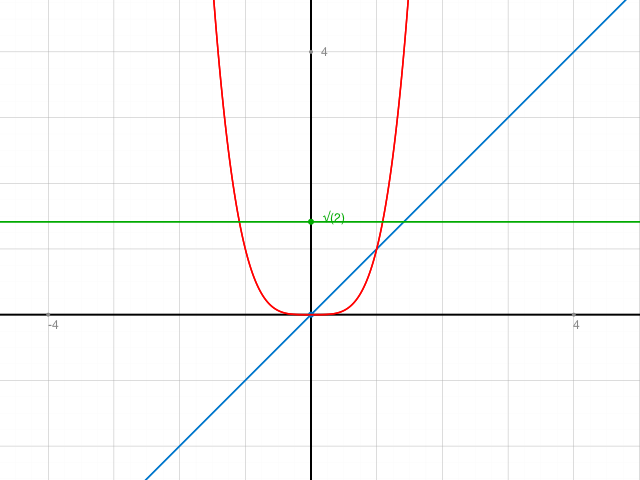
Bei g3, g4 (und g1) kann man die Graphen der Funktionen aufzeichnen. Die Mengen Zi muss man auf der y-Achse eintragen. Dann schaut man, welche dieser Werte als Funktionswerte vorkommen und bestimmt den entsprechenden Ausschnitt aus dem Urbildbereich.
Bsp g3 (rot) läuft nie unter die x-Achse. Keine Zahl aus (-∞ , 0) als Bild kommt vor. Darum ist Z3 = {} leere Menge.
g4 (grün) hat immer den y-Wert √2. √2 ist in [-2,2] enthalten. Z4 müsste also R sein. Das ist allerdings keine Funktion.
g1 : { ℕ→Ζ ; x→x}. Z1:= g1-1(Z\{1}). Hier ist der Urbildbereich nur N. Der Graph (blau) sollte nur aus den Punkten (1,1), (2,2,) … bestehen. Lässt man nun bei den Bildwerten die 1 weg, kommt man nur noch zurück auf 2,3,4,5… Deshalb gilt Z1 = N\{1}
g2: {{ M ⊂ ℕ : M endlich} → ℕ ; M → |M|} g2 berechnet die Mächtigkeit (Anzahl Elemente) von endlichen Teilmengen M von N. Das ist ein Funktion, die nicht umkehrbar ist.
Z2:=g2-1({0}) Z2 = Menge aller Teilmengen von N mit 0 Elementen. Das ist nur die leere Menge.
Somit enthält die Menge Z2 genau als einziges Element die leere Menge. Also: Z2 = {{}}