Kathetensatz: Berechne h und e eines gleichschenkligen Trapezes mit b = d = 4,0 cm; a = 8,4 cm; c = 3,6 cm

Question

Aufgabe mit Kathetensatz:

Berechne h und e eines gleichschenkligen Trapezes mit b = d = 4,0 cm; a = 8,4 cm; c = 3,6 cm.

Zeige durch eine Rechnung, dass das Teildreieck ABC nicht rechtwinklig ist. e ist die Diagonale AC.

Answer 1

ich weiss nicht genau was für dich e ist, aber bei dem anderen kann ich dir vielleicht helfen. Zunächst habe ich noch ein paar Hilfsgrößen eingfügt. Was du ausnutzen musst ist, dass b und d gleich groß sind und du damit ein gleichschenkliges Trapez hast.

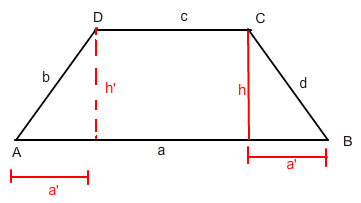
Um jetzt h zu berechnen muss du zuerst a' berechnen:

Dabei ist a'=(a-c)/2.

Dann kannst du den Winkel in B (bzw. A) berechnen mit Hilfe des Cosnius. Wenn du dann nochmal den Sinus auf B anwendest, bekommst du die Größe h.

Ich hoffe ich konnte dir erstmal helfen.

Comments

Die Höhe kann man auch über den Pythagoras berechnen... (Man sieht das schön an deiner Zeichnung)

---

Wenn ich "a" und "h" habe, wie berechne ich "c"? Geht das überhaupt, wenn ja, wer kann mir hier einen Tip geben?

---

Aus "a" und "h" lässt sich leider kein "c" berechnen, denn mit "a" und "h" lässt sich nur ein teilweise bestimmtes Dreieck (2 Elemente definiert, Seite und Seite) bilden. Da "c" nur diese Dreiecke verbindet, kann diese Grösse unendlich gross sein. Möchtest du c Berechnen, dann benötigst du mindestens eine Seite, die "c" enthält, sei es eine Diagonale oder "c"+"a".

Answer 2

wenn ich "a" und "h" habe, wie berechne ich "c"?. Geht das überhaupt, wenn ja, wer kann mir hier einen Tip geben?

Geht nicht, denn c ist durch a und h nicht bestimmt, siehe Skizze

gleiche Werte für a und h aber c offenbar verschieden