Berechnen Sie den Inhalt der Fläche und das Volumen: f(x)=x1/5 und g(x)=x2/3.

Question

ich muss die Fläche und das Volumen der folgenden Funktionen ausrechnen: (mit Hilfe des Integrals)

f(x)=fünfte wurzel aus x und g(x)=x²/3.

Bin wieder mal hilfslos! (Ich mache gerade Abitur online, d.h. wir müssen uns vieles selber aneignen. Wenn man jedoch das Thema nicht zuerst im Unterricht erklärt bekommt und im Internet auch nichts findet, dann ist man total aufgeschmissen...). 

Deshalb bin ich froh, dass diese Seite existiert und möchte allen danken, die sich Zeit zum Antworten nehmen!!!

Comments

Ist da eine Skizze dabei, der man entnehmen kann, wo diese Fläche begrenzt ist? Das wären vertikale oder horizontale Geraden. ???

Normalerweise sollte diese Aufgabe präziser gestellt sein.
Z.B. die Fläche, die zwischen den beiden Kurven eingeschlossen ist und das Volumen des Rotationskörpers, der entsteht, wenn diese Fläche um die x-Achse (vielleicht y-Achse) rotiert.

---

Leider gibt es keine Skizze dazu, aber die Aufgabe lautet so:

a) Berechnen Sie den Inhalt der Fläche, die die beiden Funktionsgraphen einschließen.

b) Berechnen Sie das Volumen des Rotationskörpers, der bei Rotation dieser Fläche um die x-Achse entsteht.

Ich hoffe, das hilft weiter.

---

Ach genau so habe ich das gelöst. Nun ist nur noch die Frage wie g(x) genau gemeint war.

Answer 1

Leider ist mir unklar wie die 2. Funktion lautet

f(x) = x^1/5 und 
g(x) = x^2/3 oder meinst du richtig x² / 3

Ich nehme mal das erste an und mache eine Skizze:

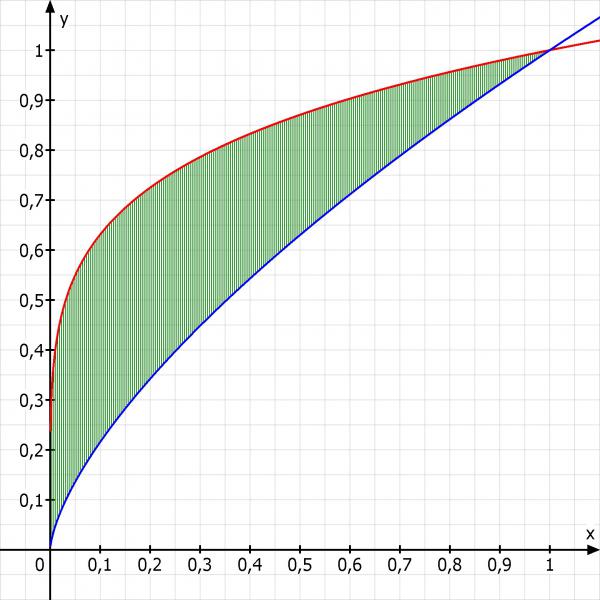
Schnittpunkte sind wie man nachweisen kann bei 0 und 1, da 0^a immer Null ist und 1^a immer 1.

Wir berechnen die Fläche

∫ 0 bis 1 (x^1/5 - x^2/3) 
= [5/6 * x^6/5 - 3/5 * x^5/3] 0 bis 1
= (5/6 * 1^6/5 - 3/5 * 1^5/3) - (5/6 * 0^6/5 - 3/5 * 0^5/3)
= 7/30

Für das Volumen nimmt man typischerweise das Rotationsintegral um die x Achse.

∫ 0 bis 1 (π·(x^1/5 - x^2/3)²) = ∫ 0 bis 1 (π·x^4/3 - 2·π·x^13/15 + π·x^2/5)
= [3/7·π·x^7/3 - 15/14·π·x^28/15 + 5/7·π·x^7/5] 0 bis 1
= (3/7·π·1^7/3 - 15/14·π·1^28/15 + 5/7·π·1^7/5) - (3/7·π·0^7/3 - 15/14·π·0^28/15 + 5/7·π·0^7/5)
= 1/14·π