f(x) = a·p/(a + (p - a)·e^{- k·p·x})
Auf einer Insel werden 1705 genau 5 Hasen gefunden.
a = 5
Tatsächlich wurden auch lange Zeit danach nie mehr als 100 Hasen gezählt. Gehe von logistischem Wachstum auf und berechne den Änderungsfaktor k.
p = 100
f(x) = 5·100/(5 + (100 - 5)·e^{-k·100·x})
f(1) = 12
f(x) = 500/(5 + 95·e^{-k·100}) = 12
k = ln((500/12 - 5)/95)/(-100) = 0.009520088144
f(x) = 500/(5 + 95·e-0.9520088144·x)
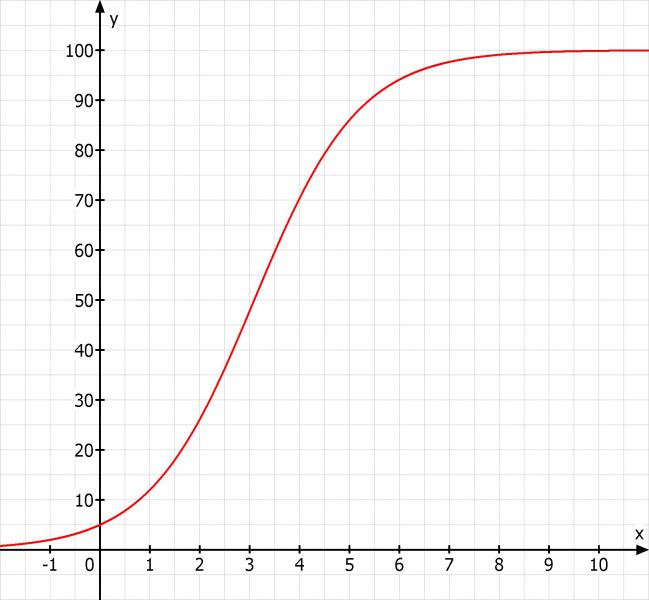
Skizze: