vielleicht kann ich dir ja auch bisschen helfen. Die a) hat ja schon der Mathecoach vorgerechnet, also mach ich mal die b)
Hier mal ein selbstgezeichnettes Bild:
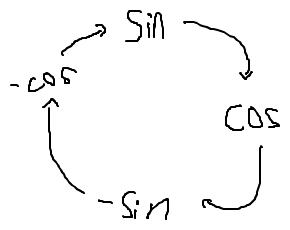
b)
f(x)= sin(4x+2)
Kettenregel anwenden, da es eine Verkettung ist:
f'(x)= 4cos(4x+2)
c)
f(x)= cos(3x2+x+1)
Auch Kettenregel anwenden:
f'(x)= -(6x+1)sin(3x2+x+1)
d)
f(x)= x2*ex
Produktregel anwenden. Ich denke ist klar warum, oder?
f'(x)= u'(x)*v(x)+v'(x)*u(x)
Wähle:
u(x)= x2
u'(x)= 2x
v(x)= ex
v'(x)= ex
f'(x)= 2x*ex+ex*x2
f'(x)= ex(2x+x2)
e)
Tipp: Produktregel und schreibe dir den Bruch mittels Potenzgesetzen um
f)
Auch die Produktregel anweden
Gruß