Zunächst mal:
x ~ t
bedeutet so viel wie proportional zu. Das heißt du kannst es auch schreiben als x = a*t. a heißt dann Proportionalitätsfaktor.
Dann machst Du Dir eine kurze Skizze der aufgeführten Funktionen mit a = 1 und der Wertetabelle:
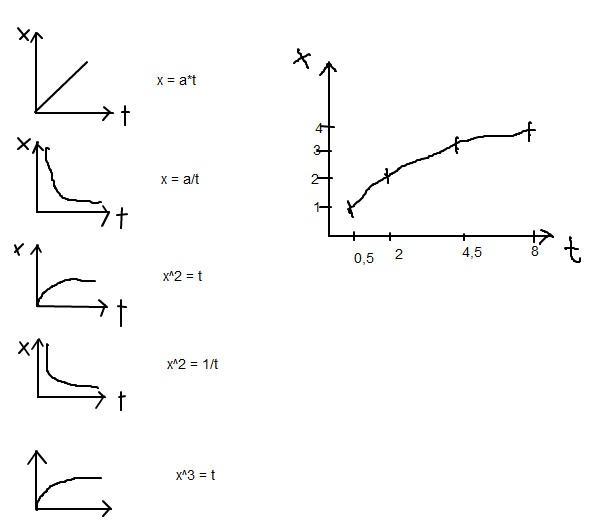
Es kommen eigentlich nur x^2 = a*t und x^3 = a*t in Frage, da ähnlicher Verlauf wie bei Wertetabelle.
Um das zu überprüfen setzt Du einfach mal ein.
a = x^2/t -> a = 2
Funktioniert auch mit allen anderen Werten, damit hast Du die Funktion gefunden.