Volumen des Wassers im Rohr mit Integral berechnen: Fliessgeschwindigkeit v(x) = 2(9-x^2)

Question

In einem Rohr mit dem Innenradius r=3cm fließt Wasser. Seine Geschwindigkeit v(m/s) hängt vom Abstand x(in cm) von der Rohrmitte ab; Es gibt v(x)=2(9-x²)

b) bestimmen Sie durch Integration das Volumen V des Wassers, das in 5 s durch eine  Querschnittsfläche des Rohrs fließt.

c) Wie groß ist die Mittlere Geschwindigkeit v des fließendes Wasser

Answer 1

Ich bin bier hier nicht ganz sicher. Wäre also gut, wenn das jemand mal checken könnte.

b) bestimmen Sie durch Integration das Volumen V des Wassers, das in 5 s durch eine  Querschnittsfläche des Rohrs fließt.

∫ _{0 bis 3} (2·pi·r·(200·(9 - r^2))) dr = 25446.9 cm^3/s = 25.45 l/s

5s * 25.45 l/s = 127.3 l

c) Wie groß ist die Mittlere Geschwindigkeit v des fließendes Wasser

25446.9 cm^3/s / (pi * 3^2 cm^2) = 900 cm/s = 9 m/s

Comments

Vielen Dank kannst nur mir bitte in Worten sagen wie du da drauf gekomme bist denn ich bin in mathe ein Idiot

---

Den Kreisumfang berechne ich mit 2 * pi * r Das multipliziere ich mit der Fließgeschwindigkeit im Abstand r. Achtung. Ich bringe die Fließgeschwindigkeit auch auf cm. Das gibt mir für jedes r die Fläche eines Zylindermantels, die durch das Rohr fließt. Das muss ich jetzt von 0 bis 3 Integrieren. Also für alle Radien, damit ich den vollen Zylinder bekomme.

---

ja ok bis dahin habe ich es verstanden das in der Klammer (200·(9 - r2))

bedeutet dr durchmesser

und bei der Aufgabe c habe ich den Ansatz nicht verstanden.  Es tut mir leid ich bin anstregend ich frage nach weil es wichtig ist.

---

das dr ist das integrationszeichen. Es heist noch normal

∫ f(x) dx

Da wir hier nicht nach x integrieren sondern nach r stehst dahinter halt ein dr. Das wird aber nicht mit berechnet. Das vor dem dr ist die Eigentliche Funktion.

---

ok danke schön aber wie sind sie auf dieses teil der Gleichung gekommen (200·(9 - r2

denn in der Aufgabe steht ja v(x)=2(9-x²) und ist das v hier als Volumen gemeint, denn es könnte auch die Geschwindigkeit sein und können Sie mir eine Formel für die Aufgabe c nennen

---

Ich bekomm ein anderes Ergebnis 127,2345025 cm3/s

---

@Anonym: Wenn ich das richtig eingegeben habe, stimmt dein Resultat nicht. vgl:

https://www.wolframalpha.com/input/?i=∫+%282·pi·r·%28200·%289+-+r2%29%29%29+dr+from+0+to+3

---

ja du hast recht @ LU könntest du mir bitte sagen wie man auf die KLammer kommt (2·pi·r·(200·(9 - r2)))  also in worten wie ich da vorgehen muss ich komme seit tagen nicht drauf danke im Voraus

---

Stell dir Gummischlauchstücke vor.

Die haben eine Mantelfläche von ungefähr  2 pi r * h

Sie sind Delta_r oder  beim integrieren dr dick.

2 pi r h dr wäre ungefähr das Volumen

Nun hast du es statt mit Gummi mit Wasser zu tun und kannst h mit deiner Geschwindigkeitsfunktion ausdrücken. In einer Sekunde kommt ja ein Wassertpartikel genau v(r) Meter weit. (Fragestellung ist hier  etwas unklar: eventuell cm?)

Daher

(2·pi·r·(200·(9 - r^2))) dr

---

ich verstehe nicht die c wieso er duch die Fläche eine kreis geteilt hat

---

Wenn alle Wasserpartikel gleich schnell fliessen würdest, würdest du ja einfach v * Querschnitt, d.h. v*Kreisfläche rechnen, um zu wissen, wie viel Wasser / Sekunde aus der Leitung fliesst.

Nun weisst du, wieviel / Sekunde rauskommt und teilst das noch durch die Kreisfläche. Das ergibt die mittlere Geschwindigkeit v.

---

Vielleicht täusche ich mich ja, aber man kann doch eine Abschätzung vornehmen. Die Geschwindigkeit ist ja so ziemlich überall gleich. [v] = m/s

Die Geschwindigkeit des Wassers am Rohrrand beträgt mit
x = r = 0,03m  und   v(x)=2 * 1/(ms) * ( 9 m^2 - x²)
v(x=r) = 17,9982 m/s
v((x=0) = 18 m/s // Maximalwert von v

Um die zurückgelegte Strecke zu berechnen rechnet man mit t₅ = 5s
v(x=r) * t₅ = h(x=r, t=5s) = 89,991m
v((x=0) *t₅ = h(x=0, t=5s) = 90m

Es gibt also keinen großen Unterschied. Deshalb sollte das Zylindervolumen bzw. das durch den Rohrquerschnitt geflossene Volumen mit guter Näherung mit A=r^2 *π der Querschnittsfläche des Rohres
h(x=0, t=5s) * A = h(x=0, t=5s) * r^2 * π = 90m * (0,03 m)^2 * π = 0,2544m^3 oder 254,4 dm^3 entsprechen.
 

Answer 2

In einem Rohr mit dem Innenradius r = 3 cm fließt Wasser. Seine Geschwindigkeit v(m/s) hängt vom Abstand x (in cm) von der Rohrmitte ab. Es gilt v(x) = 2 * (9 - x²).

Vorbetrachtung:
r = 3 cm = 0,03 m
[v] = m/s
A = r^2 * π //Querschnittsfläche des Rohres
 

Da die Angabe hier ungenau ist, zwei Fälle:

1. Fall:
v(x) = 2 * 1 / (s*m) * (9 m^2 - x^2)
Das Wasser hat hier in der Mitte des Rohrs die höchste Geschwindigkeit: v(x=0) = 18 m/s.
Am Rand beträgt die Geschwindigkeit: v(x=0,03m) = 17,9982 m/s.

2. Fall:
v(x) = 2 * ( m / (s*cm^2) ) * (9 cm^2 - x^2)
Das Wasser hat hier in der Mitte des Rohrs die höchste Geschwindigkeit: v(x=0) = 18 m/s.
Am Rand beträgt die Geschwindigkeit: v(x=0,03m) = 0 m/s.



b) Bestimmen Sie durch Integration das Volumen V des Wassers, das in 5 s durch eine  Querschnittsfläche des Rohrs fließt

1. Fall:
Da der Geschwindigkeitsunterschied zwischen Mitte und Rand minimal ist, vermute ich, dass eine näherungsweise Rechnung ausreicht. Um diese Vermutung zu bestätigen berechne ich das Volumen für den Fall, dass das Wasser mit der kleinsten und mit der größten Geschwindigkeit auf dem gesamten Querschnitt fließt.

V_max = v_max * t * r^2 * π = 18m/s * 5s * (0,03m)^2 * π = 0,2545 m^3 = 254,5 dm^3 = 254,47 L

V_min = v_min * t * r^2 * π = 17,9982 m/s * 5s * (0,03m)^2 * π = 254,44 L

V_diff = V_max -  V_min = 0,03 L = 30 mL

Bezogen auf V_max:    V_diff  /  V_max = 0,012%
Damit ist gezeigt, dass der Fehler, den man macht, minimal ist, wenn man nur näherungsweise rechnet.


2. Fall:
Integration mit Zylinderkoordinaten.

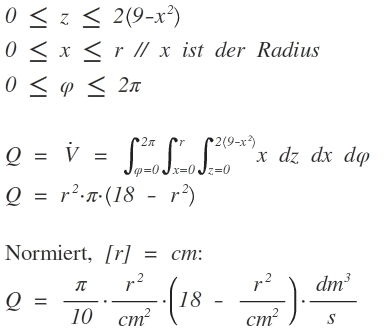
Q heißt Volumenstrom.

V = Q * t = 127,3 l/s bestätigt also das Ergebnis von Mathecoach.

Anmerkung zur Integration:
Ich verwende für die Integration Zylinderkoordinaten. In z-Richtung wird das Volumen durch die Parabel begrenz, in x-Richtung durch den Rohrradius r und es wird über den gesamten Kreis integriert 0 ≤ φ ≤ 2π.

c) Wie groß ist die mittlere Geschwindigkeit v des fließenden Wassers

Q/A = 90 dm/s = 9 m/s. Bestätigt das Ergebnis von Mathecoach.