Maximaler Wertebereich der Funktion bestimmen

Question

Wie bestimmt man den maximalen Werteberiech dieser Funktion?

$f(x)=\frac{x^{3}}{x^{2}-a}, \quad(a>0)$

Answer 1

Es gibt verschiedene Methodern dies festzustellen

Hier mit Polynomdivision

x³ : x² - a = x  + a/x + a² / [ x * (x² -a)]

lim x −> ±∞ [ x  + a/x + a² / [ x * (x² -a)] ] = x

lim x −> ∞  = ∞
lim x −> -∞  = -∞

D = ℝ

Comments

Vielen Dank, und noch eine Frage zu dieser Funktion: wie bestimme ich die  Asymptotische Verhalten hier?

---

Dies ist die Asymptote

a ( x ) = x

Das heißt : die Funktion f ( x ) nähert sich der
Funktion a ( x ) an.

---

Wird es dann richtig  wenn ich (um das Verhalten zu bestimmen) den Grenzwert für  x gegen ±∞ bestimme und  auch x gegen ±a ( Definitionslücken)?

---

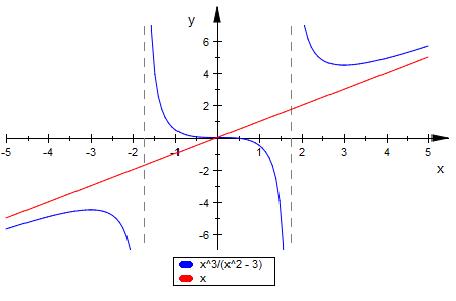
Es gibt  2 weitere Asymptoten

Der Nenner des Bruchs ( x² - a ) verursacht 2 Polstellen.
a ist laut Definition stets ein positiver Wert.

( x² - a ) = 0
x² = a

Asymptoten

x = + √ a
x = - √ a

Grenzwerte für x = + √ a

Annäherung von links :

lim x −> + √ a (-)  [   x³ / ( x² - a ) ]
( x² ist etwas kleiner als a : also eine negative 0  )
√ a )³  / 0(-) = - ∞

Annäherung von rechts :
lim x −> √ a (+)  [   x³ / ( x² - a ) ]
( x² ist etwas größer als a : also eine positive 0  )
√ a )³  / 0(+) = + ∞

Dasselbe müßtest du für x = - √ a auch machen

---

alles klar, vielen das für so eine ausführliche Erklärung!

Answer 2

Du hast eine schiefe Asymptote (Zählergrad um 1 größer als der Nennergrad). Zudem sowieso einfache Polstellen, also mit Vorzeichenwechsel.

--> Der Wertebereich umschließt alle reellen Zahlen.

Grüße