Im heutigen Artikel erkläre ich euch den Differenzquotienten, auch h-Methode genannt.
Der Differenzquotient beschreibt erstmal eigentlich eine Sekante durch zwei Punkte (x0|f(x0)) und (x1|f(x1)) des Graphen f(x). Beispiel:
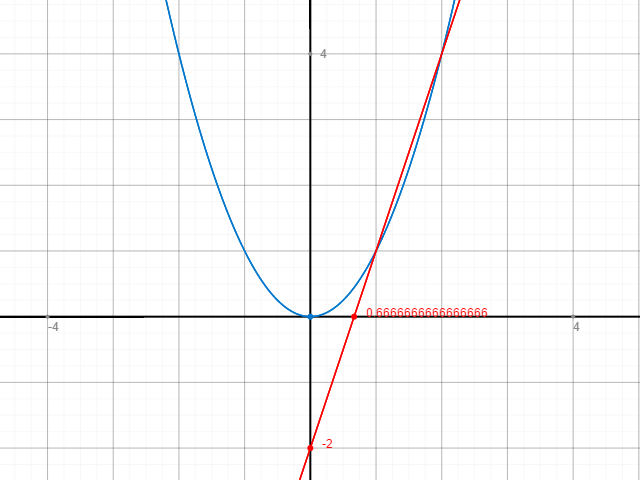
Das heißt: Wenn man die Ableitung bilden will, so nimmt man sich eigentlich erstmal zwei Punkte des Graphen, durch die die Sekante verlaufen soll. Eine Sekante schneidet den Graphen in zwei Punkten. Nehmen wir mal f(x) = x². Dort hast du dann die Punkte f(1) = 1, also A(1|1) und f(2) = 4, also B(2|4). Nun willst du die Ableitung des Graphen bestimmen. Die Ableitung gibt die Steigung in einem Punkt P an. Zwischen den x- und y-Werten der Punkte A und B ist ja jetzt eine gewisse Differenz, nämlich Delta x bzw. Delta y (wobei das Delta für Differenz steht). Nun schieben wir den einen Punkt B unendlich nah an den Punkt A. Die Differenz wird immer kleiner und h:= x1-x0 strebt gegen Null
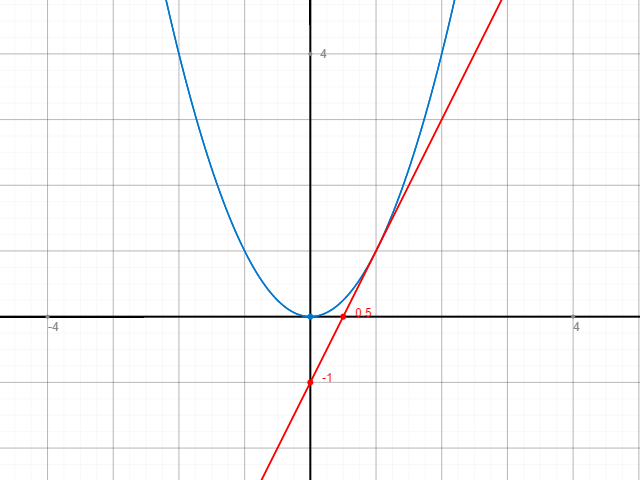
Dieses Prinzip sorgt dafür, dass wir statt einer Sekanten quasi eine Tangente haben. Eine Tangente ist dabei eine Funktion, die den Graphen f(x) in genau einem Punkt berührt. Und durch dieses Prinzip können wir nun mit Hilfe des Differenzquotienten die Ableitung am Punkt A bestimmen.
Nehmen wir uns mal die Formel für diesen her:
$$ \lim_{h\to 0} = \frac { f(x_0+h) -f(x) }{ h }$$
wobei h ja wieder diese unendlich kleine Differenz ist. deshalb hab ich ganz am Anfang lim (h->0) geschrieben. Das bedeutet h strebt gegen Null, und lim bedeutet Limes (also Grenzwert).
Diese Formel ist wie folgt entstanden.
Erstmal definieren wir uns Delta y und Delta x:
$$ Δx := x_1-x_0 $$
$$ Δy := f(x_1)-f(x_0) $$
Die Steigung der Sekante ist also:
$$ \frac { Δy }{ Δx } = \frac { f(x_1) -f(x_0) }{ x_1 - x_0 }$$
Wir definieren und setzt ein neues h und ein neues x mit
$$ x = x_0 +h \\ h = x_1 - x_0 $$
Das setzen wir entsprechend ein und erhalten:
$$ \lim_{h\to0} = \frac { f(x_0+h) -f(x) }{ h }$$
Dies ist der sogenannte Differenzquotient.
Jetzt brauchen wir unsere Funktion: f(x) = x². Also ist unsere Ableitung:
$$ f'(x) = \lim_{h\to0} \frac { (x+h)^2 -x^2 }{ h } \\ = \lim_{h\to0} \frac { x^2 +2hx +h^2-x^2 }{ h } \\ = \lim_{h\to0} \frac { 2hx +h^2 }{ h } \\ = lim(h->0): (2x+h) \\ = \lim_{h\to0} 2x $$
Wir haben ja gesagt, h strebt gegen Null. Deshalb ist es hier möglich, in den Nenner quasi Null einzusetzen, da es ja nicht ganz genau Null ist, sofern man das braucht. Die Abweichung ist hier so schwindend gering, weshalb das hier klappt. Ich erläutere eben meine Rechnung:
- Zunächst setzt du einfach für f(x) beim x einfach x+h ein. So erhältst du (x+h)².
- nun noch im Zähler f(x), also x² subtrahiert und das Ganze durch h geteilt.
- Jetzt habe ich die Klammer im Zähler nach der ersten binomischen Formel ausmultipliziert: (x+h)² = x² +2hx +h². Ich habe dann das x² einfach "weg gestrichen", weil ja am Ende des Zählers noch "-x²" steht und x²-x² = 0 ist.
- Jetzt habe ich h gekürzt. wenn man den verbleibenden Term nimmt, kann man das wie folgt umschreiben:
$$ \lim_{h\to0} \frac { 2*h*x + h*h }{ h } $$
$$ = \lim_{h\to0} \frac { h(2x+h) }{ h } $$
$$ = \lim_{h\to0} \frac { h }{ h }\cdot(2x+h) $$ $$ = \lim_{h\to0} 2x+h $$ Das heißt, ich habe einfach das h im Zähler ausgeklammert. Das darf man ja, wenn beide Summanden den gleichen Faktor enthalten. Schließlich habe ich noch h gekürzt, denn mal h durch h hebt sich auf (weil es gegensätzliche Rechenoperationen sind).- Zum Schluss habe ich für h Null eingesetzt. Wie gesagt, h ist eigentlich nicht genau Null. Aber diese Abweichung ist so schwindend gering, dass man dies vernachlässigen kann. Deshalb ist deine Ableitung von f(x) = x² einfach f'(x) = 2x. Ich könnte dir das dahinter stehende Rechengesetz auch beweisen, aber das würde an dieser Stelll zu weit führen.
- Um jetzt die Steigung zu bestimmen, setzt du einfach nur den x-Wert von A in diese Gleichung ein, und die Steigung im Punkt A ist also 2x = 2 * 1 = 2.
Ich hoffe der Tipp hat einigen geholfen :)