Extremwertaufgabe: Kreis ein möglichst grosses Rechteck einbeschreiben.

Question

,

kann mir Bitte jemand mit der Aufgabe Helfen, am besten mit nachvollziehbarem Rechenweg!?

Aufgabe: In einen Kreis (r=15cm) soll ein Rechteck mit möglichst großem Flächeninhalt einbeschrieben werden. Wie groß sind die Rechtecksseiten?

Answer 1

Hier zunächst die Skizze

Es gilt der Pythagoras

r² = x² + y²
y = √ ( r² - x² )
y ist der Funktionswert f ( x )

Ein Rechteck hätte den Flächeninhalt
A ( x ) = x * f ( x )
A ( x ) = x * √ ( r² - x² )
A ( x ) = x * √ ( 15² - x² )
A ( x ) = x * √ ( 225 - x² )
1.Ableitung bilden um den Extremwert ( Max ) zu ermitteln
A ´( x ) = 1 * √ ( 225 - x² ) + x * ( -2x ) / ( 2 * √ ( 225 - x² ))
A ´( x ) = √ ( 225 - x² ) - x ²  / √ ( 225 - x² )

√ ( 225 - x² ) - x ²  / √ ( 225 - x² ) = 0
√ ( 225 - x² ) = x ²  / √ ( 225 - x² )
( 225 - x² ) = x²
2*x² = 225
x = 10.6

f ( 10.6 ) = √ ( 15² - 10.6² )
f ( 10.6 ) = 10.6

Das Rechteck ist ein Quadrat und hat die Maße 10.6 * 10.6.

mfg Georg

Comments

Ich hab mal noch eine kleine Frage, muss ich 10,6 noch mal 4 rechnen?

---

Habe ich übersehen.
Die Seitenlänge von 10.6 gilt für den 1.Quadranten.
Das Quadrat im Vollkreis hat die Seitenlängen 21.2 * 21.2 .

---

Ok, dann noch eine winzige Frage sind das cm oder cm² ?

Ich Danke dir für deine Hilfe ;D

---

Alle Längen / Angaben in cm.
Rechteckseite : 21.2 cm

---

Ok und das Ergebnis ist cm oder?

---

Die Frage der Aufgabenstellung war :

Wie groß sind die Rechtecksseiten?

Die Antwort ist

Die Rechteckseiten sind jeweils 21.2 cm.

Nach der Größe der Fläche wurde nicht gefragt.
Diese ist : 21.6 cm * 21.6 cm = 466.56 cm^2.

Answer 2

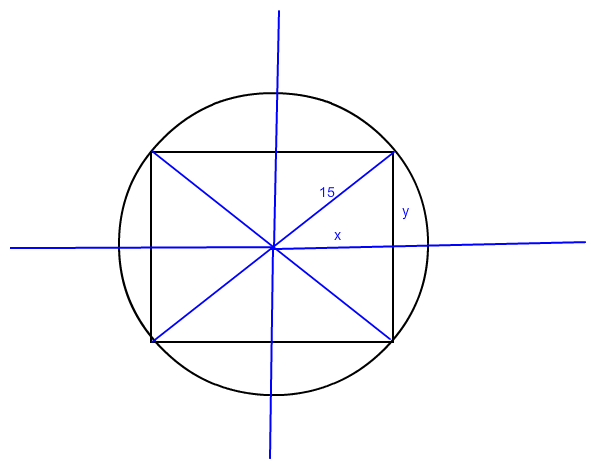
y = √(15² -x²)

F(x) = 4*x*√(15² - x²)  soll maximiert werden.

Vereinfachungen der Rechnung

4 kann man weglassen, da es genügt, das kleine Rechteck rechts oben zu maximieren.

g(x) = x√(15² -x²)          maximieren.

Wenn man die Maximalstelle sucht ist, es egal, ob man g(x) oder (g(x))² maximiert. Zudem ist dann die Wurzel weg.

h(x) = (g(x))² = x²(15² - x²)

= 225x² - x⁴

Davon nun Extremalstelle bestimmen. 

h'(x) = 450x - 4x³ = 0

x(450 - 4x²) = 0

x=0 gibt eher ein Minimum.

450= 4x²

x = √(225/2) = 15/√2

y=√(225 - 225/2) = 15/√2

Es kommt somit ein Quadrat raus mit den Seitenlängen.

2x = 2y = 15*√2

Comments

Gibt es hier eine Nebenbedingung?

---

Pythagoras aus Skizze. Hatte ich gleich vorgezogen in:

y = √(15² -x²)