Wie lautet der Funktionsterm von K?

Question

Bitte um Hilfe !! Das Schaubild von K mit f(x)=(ax+b)e^{x} berührt y=e in x=1  Gesucht ist der Funktionsterm! LG

Answer 1

y=e ist eine Gerade, die parallel zur x-Achse verläuft, also Steigung 0.

Also  f ' ( 1) = 0   und f (1 ) = e  [ Damit der Funktionswert stimmt.]

f ' (x) = ( ax + a+b ) e ^x  

also   (a + a + b) * e  = 0      und   (a+b) * e = e
                                                           gibt a+b = 1
                                                                             b = 1-a
           ( a + a +1 - a) * e = 0
                           a+1 = 0
                           a = -1                                     b = 2
Also f(x) = ( -x+2)*e^x  

Answer 2

f(x)=(ax+b)e^x berührt y=e in x=1

Du hast 2 Funktionen
f ( x ) = ( a * x+b ) * e^x
y = e ( Eine Gerade mit Abstand e zur x-Achse und der Steigung 0 )

Das wichtigste in der Aufgabenstellung ist das Wort
" berührt ". Es ist ein Berührpunkt für den gilt

f ( x ) = y
f ´( x ) = y ´

f ´( x ) = a * e^x + ( a * x + b ) * e^x
f ´( x ) = e^x * ( a * x + b + a )

( a * x + b ) * e^x = y
( a * 1 + b ) * e^1 = e
a + b = 1

e^x * ( a * x + b + a ) = y ´
e^1 * ( a * 1 + b + a ) = 0
e * ( 2 * a + b ) = 0
Ein Produkt ist dann 0 wenn mindestens 1 der Faktoren 0 ist.
2 * a + b = 0

a + b = 1
2 * a + b = 0

b = 1 - a
2 * a + ( 1 - a ) = 0
a + 1 = 0
a = -1
b = 1 - (-1)
b = 2

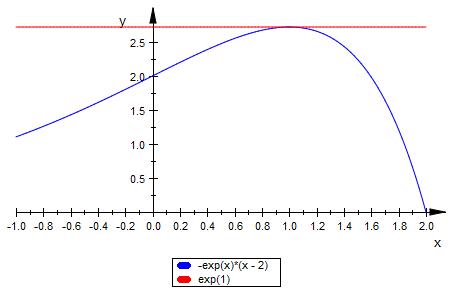
f ( x ) = ( -1 * x + 2 ) * e^x