Bestimmen Sie einen möglichen Funktionsterm aus der Abbildung.

Question

Aufgabe:

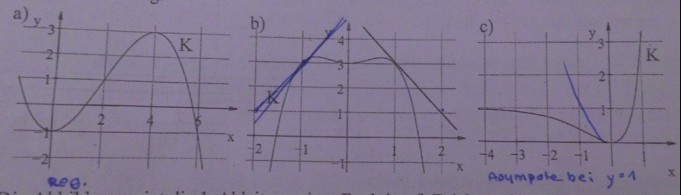
K ist das Schaubild einer Funktion f. Bestimmen Sie einen möglichen Funktionsterm aus der Abbildung.

Ansatz/Problem:

a) und b) habe ich gelöst und würde mich über Rückmeldung/Korrektur freuen.

a) -0,125 x ^{3} + 0,75 x^{2} -1 (mit GTR -> Statistik Menü -> Regression)

b) y= -x^{4} + x^{2} + 3 (Bedingungen augstellt und dann im Equa-Menü ; GTR)

Könnte mir für Aufgabe c jemand zeigen, was man machen muss (Vermutung: e-Funktion)

Wir machen wir das nur mit GTR und legen grundsätzlich immer den Schwerpunkt auf den GTR.

Comments

Bei der c) würde ich mal was "brüchiges" annehmen, im Nenner müsste eine Funktion sein, die bei negativen Werten unendlich wird, aber bei positiven x gegen einen festen Wert läuft.

Im Zähler brauchen wir eine Funktion, die bei x=0 brav Null wird. Das tut zu ersten Testzwecken auch mal schon eine Gerade durch den Ursprung.

Um solche Modellierungen "kreativ" durchführen zu können, muss man die Kurvendiskussion sehr gut beherrschen und dan praktisch "umdrehen", also wissen, wie eine Funktion aussehen sollte, um eine Bedingung zu erfüllen.

Answer 1

zu c)

Hab mal ein bisschen rumprobiert und bin zu der Lösung gekommen:

\( f(x)=\frac{x-|x|}{2 x} · \frac{1}{2} \sqrt{\frac{x-|x|}{2 x} · (-x)}+\frac{-x-|x|}{-2 x} · 3 x^{2} \)

Kann natürlich sein, dass was ganz anderes gemeint ist, aber das Schaubild geht auch durch die Punkte (-4I1), (0I0) und (1I3) und auf meinem Gtr sieht es auch so aus wie auf dem Bild.

Answer 2

Ich hatte den Graphen schon einmal
irgendwo gesehen. Ein normaler Mensch kommt auf
so etwas nicht. Du mußt noch ein bißchen anpassen.

Answer 3

Anderer Vorschlag. Hier wäre auf x=1 eine Asymptote.

Linken Teil des zweiten Graphen betrachten.

Etwas einfacher zu sehen ist das vermutlich hier:

Passt somit auch nicht 100%ig.

Das folgende Bild wäre von f(x) = x^2 / (x-1.5)^2

Comments

Danke, ich suche noch grade meinen GTR aber vielleicht könnte es  x^2/e^x sein?
Ansonsten ist deine Angleichung sehr gut, danke

---

b) y= -x⁴ + x² + 3 

Symmetrie.

Ansatz y= ax^4 + bx^2 + c, wobei y-Achsenabschnitt 3 schon mal c=3 festlegt.

Nun hast du 2 Nullstellen 1.5 und -1.5

Daher: f(x) = (1.5 + x)*(1.5 -x)*(....?)

= (2.25 - x^2)( p + qx^2) 

Wobei 

2.25 * p = 3 wegen y-Achsenabschnitt.

Also p=4/3

Daher f(x) = (2.25 -x^2)(4/3 + qx^2) 

Nun noch P(1|3) einsetzen.

3 = (2.25 -1)(0.75 + q)

3 = 1.25(4/3 + q)

q = 16/15

Daher

f(x) = (2.25 -x^2)(4/3 + 16/15* x^2) 

Kontrolle: https://www.wolframalpha.com/input/?i=+%282.25+-x%5E2%29%284%2F3+%2B+16%2F15*+x%5E2%29+

a und b liegen ganz nahe bei deinen a und b.

---

Das Problem bei x^2 * e^x ist, dass das eine horizontale Asymptote bei y=0 hat und nicht bei y=1.

EDIT: Deine Antwort bei a) überzeugt. vgl. https://www.wolframalpha.com/input/?i=+-0.125+x+%5E3+%2B+0.75+x%5E2+-1

Wenn du rechnen willst, leg den Koordinatenursprung in den Wendepunkt.

setze an y = a x^3 + bx 

nun gilt y(2) = 2. ==> 2 = 8a + 2b ==> 2- 8a = 2b       (I)

und y(4) = -2 ==> -2 = 64a + 4b ==> -1 = 32a + 2b        (II)

(I) in (II) ==> -1 = 32a + 2 - 8a

-3 = 24a

-1/8 = a

2b = 2 -8a = 2+1 

b = 3/2 

Also y = -1/8 x^3 + 3/2 x

nun 2 nach rechts und 1 nach oben schieben.

y = -1/8 (x-2)^3 + 3/2 (x-2) + 1

Klammern auflösen gibt exakt deine Gleichung. Vgl. auch https://www.wolframalpha.com/input/?i=-1%2F8+%28x-2%29%5E3+%2B+3%2F2+%28x-2%29+%2B+1

Answer 4

$$ \zeta(x)= \left(e^x+\frac{4}{\pi^2}\right) \cdot \left(\arctan(x)\right)^2 $$

passt ganz gut finde ich ...