Barockgiebel: Rand in Form einer ganzrationalen Funktion.

Question

Aufgabe - Berechnungen am Barockgiebel:

Der symmetrische Giebel eines Barockhauses soll rekonstruiert werden. Der Giebel ist in der Abbildung in einem Koordinatensystem dargestellt. Eine ganzrationale Funktion \( f \) beschreibt im entsprechenden Intervall den oberen Giebelrand. Die x-Achse ist die Tangente an den Graph der Funktion \( f \) in den Punkten \( P_{1}(-4 \mid 0) \) und \( P_{2}(4 \mid 0) \).

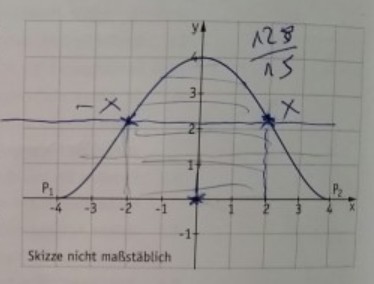
10.1 Begründen Sie, dass f eine Funktion mindestens 4. Grades sein muss.

10.2 Ermitteln Sie eine Gleichung der Funktion \( f \).

10.3 Ein Architekt beschreibt einen solchen Giebelrand durch die Funktion \( \mathrm{g} \) mit \( g(x)=\left(\frac{1}{8} x^{2}-\left.2\right)^{2}\right. \). Dieser Giebel soll durch eine waagerechte Linie in zwei flächeninhaltsgleiche Teile zerlegt werden. Während der untere Teil des Giebels mit Ornamenten verziert wird, ist beabsichtigt, im oberen Teil des Giebels Fenster anzubringen.

Ermitteln Sie auf Dezimeter genau, bis zu welcher Höhe der Giebel mit Ornamenten versehen werden soll.

Ansatz/Problem:

Ich habe Probleme mit der Teilaufgabe 10.3.

Answer 1

f(x) = (1/8·x^2 - 2)^2

∫ (0 bis 4) ((x^2 - 16)^2/64) dx = 128/15

k·f(k) + ∫ (k bis 4) ((x^2 - 16)^2/64) dx = 64/15

3·k^5 - 80·k^3 + 1024 = 0

k = 2.572555128

f(k) = 1.375330868

Beim Lösen musste ich ein Näherungsverfahren benutzen. Vermutlich geht es nicht anders, denn in der Aufgabenstellung steht ja bereits man soll eine Näherung angeben.