Geradengleichung und Größe des Schnittwinkels bestimmen

Question

Ich bräuchte etwas Hilfe bei einer Aufgabe.

Gegeben ist die Funktion f(x)=-1/2x²+2x+2

a) Eine Gerade durch den Punkt P(-1|0) schneidet den Graphen von f an der Stelle x=3. Geben Sie die Geradengleichung und die Größe des Schnittwinkels an.

-> Ich habe keine Ahnung wie ich vorgehen muss, also für x 3 einsetzen, würde ich mal vermuten aber was dann? Wäre sehr über Hilfe dankbar.

.

Comments

Geradengleichung ---- > erst m ----->  m =  y2 - y1  /  x2 - x1  

m =  12 - 0 /  3 -( -1 )  =  12 /4 =  3  !

y = 3*x +n   , nun n bestimmen →  12=  3  *  3  +n    ,    n =  12 - 9 = 3

y =  3x + 3  !!

Woher kommt die 12? Das wäre dann ja y2, aber das ist ja nicht gegeben, wie kommt man daruaf?

Und wie berechne ich dann den Schnittwinkel?

Answer 1

Geradengleichung ---- > erst m ----->  m =  y2 - y1  /  x2 - x1  

m =  12 - 0 /  3 -( -1 )  =  12 /4 =  3  !

y = 3*x +n   , nun n bestimmen →  12=  3  *  3  +n    ,    n =  12 - 9 = 3

y =  3x + 3  !!

Comments

Okay, aber woher kommt die 12?

---

Die Antwort ist leider falsch.

Answer 2

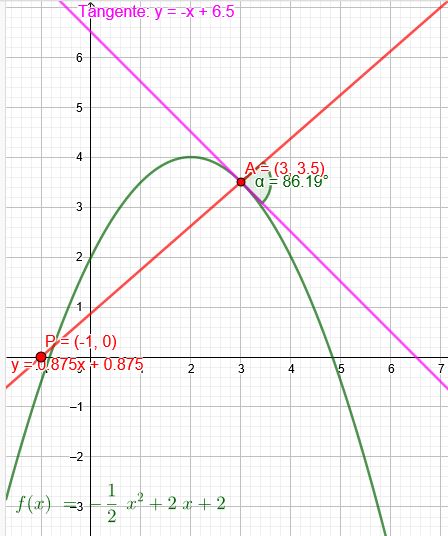
Gegeben ist die Funktion $f(x)=-\frac{1}{2}x^2+2x+2$
a) Eine Gerade durch den Punkt P$(-1|0)$ schneidet den Graphen von f an der Stelle $x=\red{3}$. Geben Sie die Geradengleichung und die Größe des Schnittswinkels an.

$f(\red{3})=-\frac{1}{2}\cdot \red{3}^2+2\cdot \red{3}+2=3,5$  → A $(3|3,5)$

Gerade durch P$(-1|0)$ und A $(3|3,5)$  :

$\frac{y-0}{x+1} =\frac{3,5-0}{3+1}=0,875$

$y=0,875x+0,875$

Bestimmung der Steigung der Tangente in   A $(3|...)$:

$f'(x)=-x+2$

$f'(3)=-3+2=-1$

Die Gerade durch P und A hat die Steigung $m_1=0,875$

Die Steigung der Tangente in A ist $m_2=-1$

Berechnung des Winkels zwischen beiden Geraden:

$\tan(α)=|\frac{m_2-m_1}{1+m_1m_2}|=|\frac{-1-0,875}{1+0,875\cdot (-1)}|=|\frac{-1,875}{0,125}|=15$

$\tan^{-1}(15)=86,19°$