"Ich habe zwei Punkte gegeben einen Hochpunkt H(3|5) und einen Wendepunkt W(4|4) und ich soll eine Polynomfunktion 3.Grades aufstellen, wie komme ich denn jetzt auf diese? "
Lösung über die Nullstellenform der kubischen Parabel:
Ich verschiebe den Graph um 5 Einheiten nach unten → H´(3|0) : doppelte Nullstelle und W´(4|-1)
f(x)=a*(x-3)^2*(x-N)
W´(4|-1)
f(4)=a*(4-3)^2*(4-N)=a*(4-N)
1.) a*(N-4)=1 → a=\( \frac{1}{N-4} \)
f(x)=\( \frac{1}{N-4} \)*[(x-3)^2*(x-N)]
f´(x)=\( \frac{1}{N-4} \)*[2*(x-3)*(x-N)+(x-3)^2]=\( \frac{1}{N-4} \)*[(2x-6)*(x-N)+(x-3)^2]
Wendepunkteigenschaft benützen:
f´´(x)=\( \frac{1}{N-4} \)*[2*(x-N)+(2x-6)+2*(x-3)]
f´´(4)=\( \frac{1}{N-4} \)*[2*(4-N)+(2*4-6)+2*(4-3)]
2.)\( \frac{1}{N-4} \)*[2*(4-N)+(2*4-6)+2*(4-3)]=0
[8-2N+4]=0
N=6 a=\( \frac{1}{6-4} \)=\( \frac{1}{2} \)
f(x)=\( \frac{1}{2} \)*(x-3)^2*(x-6)
und nun wieder 5 Einheiten nach ober verschieben:
p(x)=\( \frac{1}{2} \)*(x-3)^2*(x-6)+5
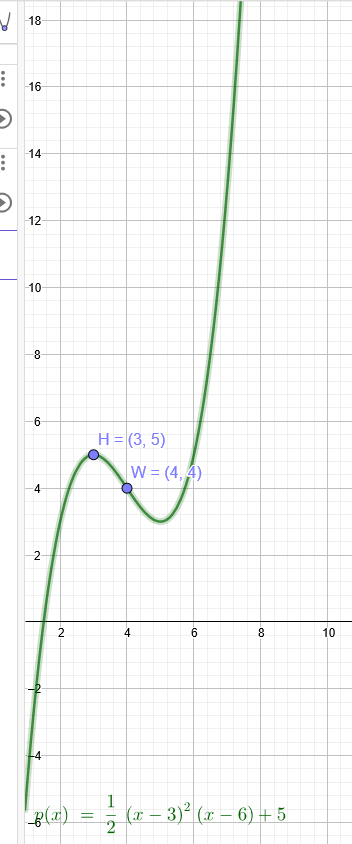
Die Wendestelle liegt bei x=4 . Die Tangente durch H (3|5) schneidet den Graphen in P . Er liegt in doppelter Entfernung sonder Wendestelle wie der Hochpunkt. P(6|5)
Beide Punkte verschiebe ich um 5 Einheiten nach unten
H´(3|0) doppelte Nullstelle und P´(6|0) einfache Nullstelle.
Linearfaktorenform:
\( f(x)=a(x-3)^2(x-6) \)
W(4|4) ↓ W´(4|-1):
\( f(4)=a(4-3)^2(4-6)=-2a=-1 \)
\(a=\frac{1}{2} \)
\( f(x)=\frac{1}{2}(x-3)^2(x-6) \) 5↑ :
\( p(x)=\frac{1}{2}(x-3)^2(x-6)+5 \)