Kegelvolumen und Quadervolumen maximieren. Extremwertaufgaben mit Nebenbedingung.

Question

Aufgabe 5:

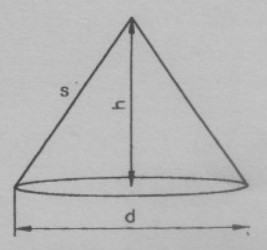
Von einem Kegel ist die Mantellinie \( s \) bekannt. Das Volumen des Kegels ist von seiner Höhe \( \mathrm{h} \) abhängig.

a) Bestimmen Sie die Funktionsgleichung \( V=f(h) \) und geben Sie den Definitionsbereich an.

b) Zeichnen Sie den Graphen der Funktion, wenn \( \mathrm{s}=2 \mathrm{~m} \) ist.

c) Für welche Höhe \( \mathrm{h} \) wird das Volumen maximal?

Aufgabe 6:

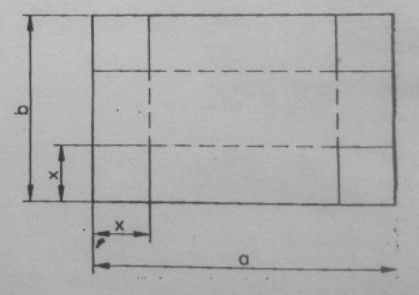
Aus einer rechteckigen Pappe soll ein nach oben offenes Kästchen gefertigt werden. Dazu werden an den Ecken Quadrate mit der Kantenlänge \( x \) herausgeschnitten.

a) Geben Sie die Funktion an, die das Volumen des Kästchens in Abhängigkeit des Maßes \( x \) angibt \( V=f(x) \).

b) Bestimmen Sie den Definitionsbereich und zeichnen Sie den Graphen, wenn \( a=20 \mathrm{~cm} \) und \( b=12 \mathrm{~cm} \) sind.

c) Für welchen x-Wert wird das Volumen maximal?

Comments

Zu 6. Verfolge mal die Links in der Rubrik "ähnliche Fragen".

Da sollte es möglich sein, dass du etwas findest, bei dem du nur noch die Zahlen ändern musst.

Etwas einfacheres Bsp. https://www.mathelounge.de/35589/quader-deckel-quadratischem-herstellen-volumen-maximieren

---

Das Volumen \(V\) eines Quaders berechnet sich allgemein gemäß der Formel
V = Länge·Breite·Höhe. Die Grundfläche deines nach oben offenen Quaders hat wie man der Skizze entnimmt die Länge \(a-2\cdot x\) sowie die Breite \(b-2\cdot x\). Die Höhe ist \(x\). Damit lautet die gesuchte Funktion$$V=f(x)=(a-2\cdot x)\cdot(b-2\cdot x)\cdot x.$$Ausmultipliziert erhältst du ein Polynom dritten Grades, dessen Extremwerte nach bekanntem Schema bestimmt werden sollen.

---

Also sind die Lösungen für

A) Nur die Formel V=A x B x C

B) V=f(x)=(a-2*x) * (b-2*x) *x

C) nur extremwerte dann berechnen

---

Nicht ganz. Die Bestimmung der Volumenfunktion \(V=f(x)=(a-2\cdot x)\cdot(b-2\cdot x)\cdot x\) gehört noch zum Aufgabenteil a). Bei der b) sollst du den Definitionsbereich für \(x\) ermitteln. D.h. du solltest dir überlegen, welche \(x\in\mathbb R\) hier sinnvoll sind. Beachte dabei, dass Länge, Breite und Höhe des Quaders nicht negativ sein können. Bei c) musst du dann noch zwischen Maximum und Minimum unterscheiden.

Der Vollständigkeit halber sei noch erwähnt, dass zu zeigen bleibt, dass das auf diese Weise ermittelte relative Maximum auch das absolute innerhalb des Definitionsbereichs ist.

Answer 1

s^2 = h^2 + (d/2)^2

V =1/3  * d^2/4 * pi * h   und  d^2/4 = s^2 - h^2

V(h) =1/3   * pi * ( s^2 - h^2 ) * h  ist die F-gl.

         = 1/3   * pi * ( h*s^2 - h^3 )

maximal ?

V ' (h) = 1/3   * pi * ( s^2 - 3*h^2 )  ist gleich 0 für h= s/ wurzel(3)

für diesen Wert von h ist das Volumen max.