ich habe mich daran versucht, die Gesamtlänge eines aufgewickelten Bandes auf einer Spule zu berechnen.
Leider komme ich auf kein befriedigendes Ergebnis über ein Integral. Ich möchte gern mein Vorgehen erläutern, in der Hoffnung das jemand meinen Fehler findet.
Zunächst die Skizze:
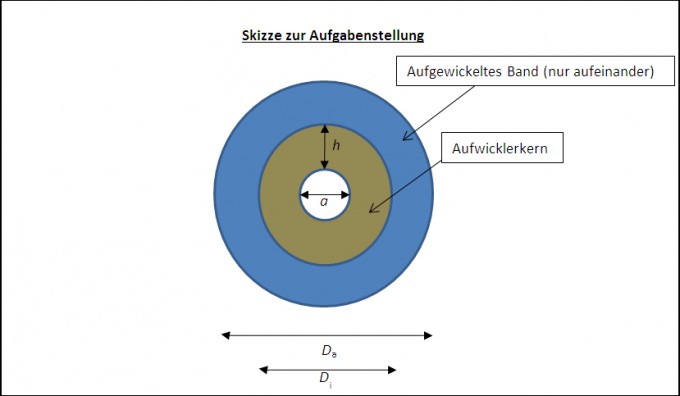
Werte:
Da =101,22mm; Di = 86,97mm; a = 75,85mm; h = 5,56mm
Die Anzahl n der Wicklungen eines Kreisrings mit dem Außendurchmesser Da, Innendurchmesser Di und Banddicke b ergibt sich aus:
$$n\quad =\quad \frac { { D }_{ a }-{ D }_{ i } }{ b } ; (1)$$ $${ D }_{ i }\quad =\quad { a }+2h;(2)$$
Der Umfang einer Wicklung von der Spule ist
$${ U }_{ n }\quad =\quad { d }_{ n }*\pi \quad =\quad { (D }_{ i }+2nb)*\pi(3)$$
Die Aufsummierung der Differenzumfänge zwei übereinanderliegender Lagen + der Umfang des Aufwicklerkerns ergibt die Gesamtlänge:
$${ l }_{ ges }\quad =\sum { U } \quad =\quad { U }_{ 0 }+\sum _{ n=1 }^{ n-1 }{ { U }_{ n }-{ U }_{ n-1 } } (4)$$
Bekomme diese Gleichung nicht weiter aufgelöst bzw. mir fehlt der Ansatz.=/
Daher wollte Ich jetzt Gleichung (3) nach n integrieren - also -
$$\sum { { U }_{ n }\quad =\quad } { l }_{ ges }\quad =\quad \pi \int _{ n=0 }^{ n }{ \left( { D }_{ i }+2nb \right) \quad dn } $$
$$<=>\left( b*{ n }^{ 2 }+{ D }_{ i }*n \right) *\pi $$
um so auch auf die Gesamtlänge zu kommen, jedoch stimmt der Wert nicht mit der Gleichung
$${ l }_{ ges }=\quad \frac { \pi }{ 4b } *\left( { { D }_{ a } }^{ 2 }-{ { D }_{ i } }^{ 2 } \right) $$ überein.
Ich finde einfach meinen Denkfehler nicht. -.-