https://www.wolframalpha.com/input/?i=f%28x%29+%3D+%282x%29%2F%28x%5E2-4%29%2C+g%28x%29%3D+%281+%2B+√%281%2B4x%5E2%29%29%2Fx+
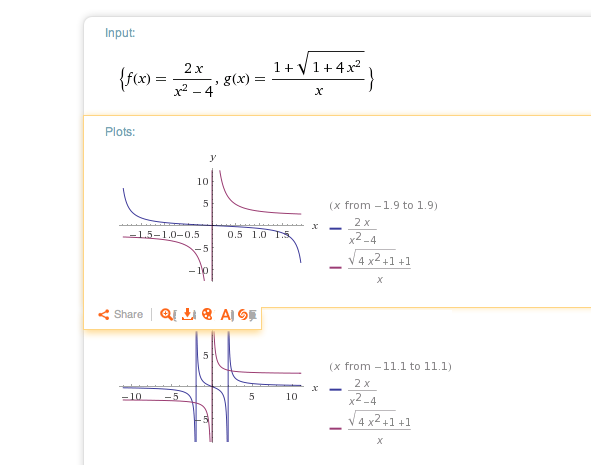
Zur Frage nach der Umkehrfunktion. Im Bereich -2 ≤ x ≤2 wir das nicht stimmen, denn die Graphen von Umkehrfunktionen sind symmetrisch bezüglich der Winkelhalbierenden im 1. Quadranten.
Graphisch sieht es aber gut aus für die Bereiche x<-2 und x> 2.
f(x) = (2x)/(x^2-4), g(x)= (1 + √(1+4x^2))/x
a) du musst erst mal einsetzen
f(g(x)) = (2(1 + √(1+4x^2))/x ))/((1 + √(1+4x^2))/x)^2-4)
und nun vereinfachen.
= (2(1 + √(1+4x^2))/x ))/((1 + √(1+4x^2))^2)/x^2)-4)
= (2(1 + √(1+4x^2))/x ))/((1 + √(1+4x^2))^2 - 4x^2)/x^2)
= (2(1 + √(1+4x^2)) ))/((1 + √(1+4x^2))^2 - 4x^2)/x)
= ((2 + 2√(1+4x^2)) ))/((1 + 2√(1+4x^2) + (1+4x^2) - 4x^2)/x)
= ((2 + 2√(1+4x^2)) ))/((2 + 2√(1+4x^2))/x)
= 1/(1/x)
= x
Beachte: Alle Funktionswerte von g(x) sind betragsmässig grösser als 2. Daher ist f nur Umkehrfunktion von g für |x|>2.
c)
lim g(x)
= lim (1 + √(1+4x2))/x
= lim (1/x + √(1+4x2))/x )
= lim (1/x + 2x√(1/(4x^2)+1))/x )
= lim (1/x + 2√(1/(4x^2)+1)) ) | Grenzübergang x gegen unendlich.
= 0 + 2√(0 + 1)
= 2