1. Betrachte das Wachstum der Wurmes in den ersten 5 Stunden nach dem Unfall !
Ansatz:
L = l*b^{t/T};
b = 2;
l = 0,001 m;
T= 15 min = 900s;
L(t) = 0,001m * 2^{t/900s};
t ∈ [0; 18 000s]
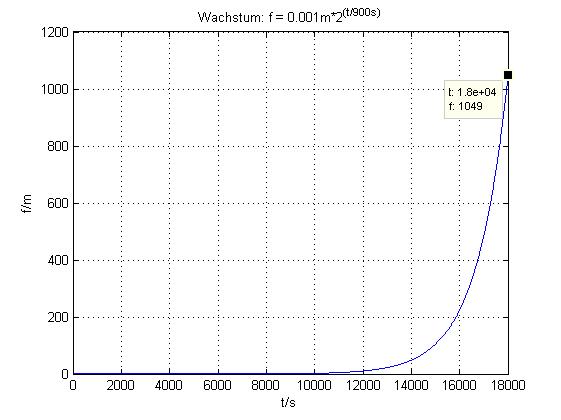
2. Nach genau 5 Stunden wird ein warnendes Funksignal zur nur einen Lichttag entfernten Erde gesendet. Das Funksignal breitet sich mit Lichtgeschwindigkeit aus, also mit 300 000 km/s. Welche Strecke legt es in 1,2,3,4,5 Stunden zurück ?
x1 = 3600s * 300 000 km/s = 1,08*10^9 km;
x2 = 1,08*10^9 km *2;
...
x5 = 1,08*10^9 km *5 = 5,4*10^9 km;
3. Wann hat das Vorderteil des Wurmes die Erde erreicht ?
L(t) = 0,001m * 2^{t/900s};
Die Raumstation ist von der Erde einen Lichttag entfernt. Das entspricht einer Entfernung x = d*c; also Dauer eines Tages mal Lichtgeschwindigkeit. Es muss also gelten :x = L(t).
d = 24*3600s = 86 400s;
c = 300 000 km/s;
Man löst nach t auf:
L = l*b^{t/T} = x;
x/l = b^{t/T};
ln(x/l) = ln(b)*(t/T);
ln(x/l) / ln(b) * T = t;
t = ln(d*c/l) / ln(b) * T ≈ 40 103,2s;
4. Konnte die Erde noch rechtzeitig gewarnt werden ?
Zeit die das Funksignal braucht:
t_funk = 5h + 24h = 104 100s; //Das Signal wird erst nach 5h gesendet und braucht einen Tag bis zur Erde
t_wurm = 40 103,2s; //Der Wurm ist also schneller
5. Wie viele Stunden ist das Funksignal unterwegs, wenn der Wurm auf die Erde trifft ?
Das Signal des Wurms erreicht nach ca. 11h die Erde. Das heißt, da das Funksignal erst nach 5h gesendet wird, dass es 6h unterwegs ist, beim Eintreffen des Wurms.
6. Wie viele km hat das Funksignal zu diesem Zeitpunkt bereits zurückgelegt und wie weit ist es noch von der Erde entfernt ?
Das Licht hat zu diesem Zeitpunkt 6*3600*300 000 km = 6,48*10^9 km zurückgelegt.
Es ist noch 24*3600*300 000 km - 6,48*10^9 km = 1,944 *10^10 km von der Erde entfernt.
7. Stelle eine Gleichung auf, mit der berechnet werden kann, zu welchem Zeitpunkt der der Erde entgegen wachsende Wurm das Funksignal überholt !
Für das Licht gilt: xL = t*300 000 km/s;
Für den Wurm gilt: L(t) = 0,001m * 2^{t/900s};
Es muss gelten: xL = L(t);
Die Gleichung lautet also:
t*300 000 km/s - 0,000 001km * 2^{t/900s} = 0;
8. Stelle eine Wertetabelle auf, mit der festgestellt werden kann, in welcher Stunde nach Aussenden des Funksignal dieses vom Wurm eingeholt wird !
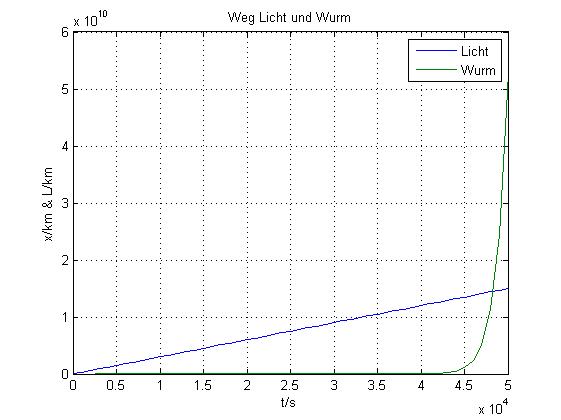

Beim Vorzeichen Wechsel (nicht der am Anfang) der Differenz überholt der Wurm das Licht.