Ermitteln Sie die Koordinaten des Punktes P, in welchem die Tangente parallel zur Sekante (AB) ist.

Question

Aufgabe:

Einleitung

Gegeben sind die Funktion f(x) = x^2 und die x-Koordinaten a, b zweier Punkte A, B des Graphen.

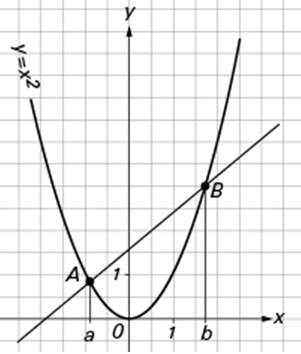
Fragestellung

Ermitteln Sie die Koordinaten des Punktes P, in welchem die Tangente parallel zur Sekante (AB) ist.

Ihre Antwort

Steigung der Sekante: m_s = ...

Steigung der Tangente: m_t = ...

Im gesuchten Punkt müssen die beiden Steigungen gleich sein: ... = ...

Damit ist der gesuchte Punkt bei: P(... | ...)

Kann mir das jemand erläutern am besten ganz einfach.

Answer 1

Ich habe es mal ausgefüllt, wie ich es verstanden habe:

Steigung der Sekante: $$ m _ { s } = \frac { f ( a ) - f ( b ) } { a - b } = \frac { a ^ { \wedge } 2 - b ^ { \wedge } 2 } { a - b } = \frac { ( a - b ) ( a + b ) } { ( a - b ) } = a + b $$

Steigung der Tangente: m_t = 2x

Im gesuchten Punkt müssen die beiden Steigungen gleich sein: 2x = a+b; x = (a+b)/2

Damit ist der gesuchte Punkt bei: $$ P(\frac{a+b}{2} | \frac{(a+b)^2}{4}) $$