Berechnen Sie die Permutation σ103

Question

Wir betrachten in der S9 die Permutation σ:

$\begin{array}{c|ccccccccc}{i} & {1} & {2} & {3} & {4} & {5} & {6} & {7} & {8} & {9} \\ \hline \sigma(i) & {5} & {7} & {2} & {9} & {1} & {3} & {6} & {8} & {4}\end{array}$

Berechnen Sie die Permutation σ¹⁰³.

Comments

Tipp: Es gilt hier: σ¹⁰³ = σ⁻¹ (warum) und daher lässt sich das Ergebnis unmittelbar aufschreiben.

---

Teilduplikat vgl hier: https://www.mathelounge.de/25491/schreiben-sie-als-produkt-von-paarw…

Answer 1

Wenn du dir das aufzeichnest, kannst du sehr schnell die Zyklen sehen.

Sigma = (15)(2763)(49)

 

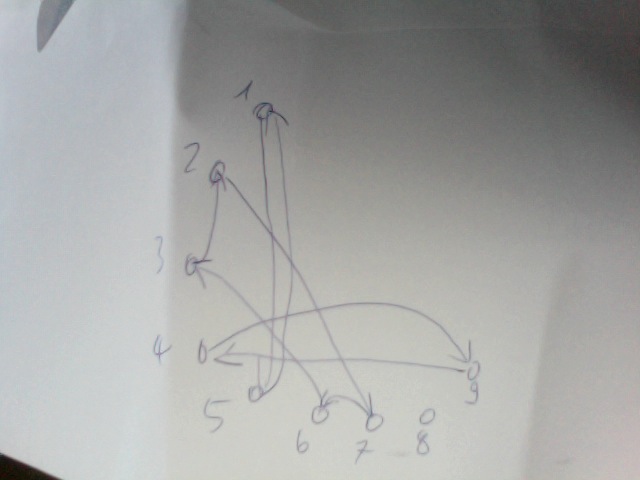
Das kgV der Zyklenlängen(2,4,2,1) ist 4. Deshalb ist sigma⁴ = Identität.

Sigma¹⁰³ = Sigma¹⁰⁰*Sigma³= Sigma³

oder einfacher Sigma¹⁰³ =  Sigma¹⁰⁴ * Sigma^-1 = Sigma^-1

Sigma = (15)(2763)(49)

Sigma¹⁰³ = Sigma^-1 = (15)(3672)(49)

Bzw. Wertetabelle von unten nach oben aufschreiben.

Answer 2

Du kannst die Permutation auch so schreiben:

(15)(2763)(49)(8)

Dann ist jede 5.Permutation wieder gleich dem Ausgang, also gilt:

\sigma^4x+1=\sigma
Jetzt ist 103/4=25+ Rest 3
und \sigma^3=\sigma^-1 also
(15)(3672)(49)(8)

Answer 3

Zuerst sollte man die Tabelle aufstellen,
123456789536917284σ^{-1}= (15)(2367)(49) σ¹⁰³ = σ⁻¹