Das macht man am besten schrittweise.
Der Kreis wird im ersten Quadranten durch die Funktion K(x) = √(1-x2) beschrieben.
Die Tangente an den Kreis in diesem Punkt (px, py) ist eine Funktion der Form t(x) = ax+b, wobei
$$ \begin{array} { l } { t \left( p _ { x } \right) = K \left( p _ { x } \right) = p _ { y } = \sqrt { 1 - p _ { x } ^ { 2 } } } \\ { t ^ { \prime } ( x ) = K^ { \prime } \left( p _ { x } \right) \quad \forall x \in R } \end{array} \\ \begin{array} { l } { K ^ { \prime } ( x ) = \frac { - x } { \sqrt { 1 - x ^ { 2 } } } } \\ { \Rightarrow K ^ { \prime } \left( p _ { x } \right) = \frac { - p _ { x } } { \sqrt { 1 - p _ { x } ^ { 2 } } } } \end{array} $$
Insgesamt lautet das Gleichungssystem für die Tangente im Punkt P also:
$$ \begin{array} { l } { a p _ { x } + b = \sqrt { 1 - p _ { x } ^ { 2 } } } \quad (I) \\ { a = - \frac { p _ { x } } { \sqrt { 1 - p _ { x } ^ { 2 } } } } \quad \qquad (II) \end{array} $$
Setzt man (II) in (I) ein, ergibt sich:
$$ - \frac { p _ { x } ^ { 2 } } { \sqrt { 1 - p _ { x } ^ { 2 } } } + b = \sqrt { 1 - p _ { x } ^ { 2 } } \\ b = \sqrt { 1 - p _ { x } ^ { 2 } } + \frac { p _ { x } ^ { 2 } } { \sqrt { 1 - p _ { x } ^ { 2 } } } $$
Die Tangente besitzt also die Gleichung:
$$ t ( x ) = - x \frac { p _ { x } } { \sqrt { 1 - p _ { x } ^ { 2 } } } + \sqrt { 1 - p _ { x } ^ { 2 } } + \frac { p _ { x } ^ { 2 } } { \sqrt { 1 - p _ { x } ^ { 2 } } } $$
Der y-Achsenabschnitt ist trivialerweise
$$ b = \sqrt { 1 - p _ { x } ^ { 2 } } + \frac { p _ { x } ^ { 2 } } { \sqrt { 1 - p _ { x } ^ { 2 } } } $$
Die Nullstelle erhält man indem man t(x0)=0 setzt:
$$ 0 = - x _ { 0 } \frac { p _ { x } } { \sqrt { 1 - p _ { x } ^ { 2 } } } + \sqrt { 1 - p _ { x } ^ { 2 } } + \frac { p _ { x } ^ { 2 } } { \sqrt { 1 - p _ { x } ^ { 2 } } } \\ x _ { 0 } \frac { p _ { x } } { \sqrt { 1 - p _ { x } ^ { 2 } } } = \sqrt { 1 - p _ { x } ^ { 2 } } + \frac { p _ { x } ^ { 2 } } { \sqrt { 1 - p _ { x } ^ { 2 } } } \quad | \cdot \sqrt { 1 - p _ { x } ^ { 2 } } \\ \begin{array} { l } { x _ { 0 } p _ { x } = 1 - p _ { x } ^ { 2 } + p _ { x } ^ { 2 } } \\ { x _ { 0 } = \frac { 1 } { p _ { x } } } \end{array} $$
Die beiden Punkte lauten also:
$$ X \left( \frac { 1 } { p _ { x } } , 0 \right) \\ Y \left( 0 , \frac { 1 } { 2 } \left( \sqrt { 1 - p _ { x } ^ { 2 } } + \frac { p _ { x } ^ { 2 } } { \sqrt { 1 - p _ { x } ^ { 2 } } } \right) \right) $$
Der Mittelpunkt der beiden kann gemäß ((x1+x2)/2|(y1+y2)/2) bestimmt werden.
Er lautet also:
M(1/2px | (√(1-px2)+px2/√(1-px2))/2)
Wählt man nun x=1/(2px), kann man das umstellen zu:
px = 1/(2x)
Eingesetzt in die y-Komponente folgt damit:
y(x) = (√(1-1/(4x2)) + 1/(4x2√(1-1/(4x2))))/2
Huihuihui. :)
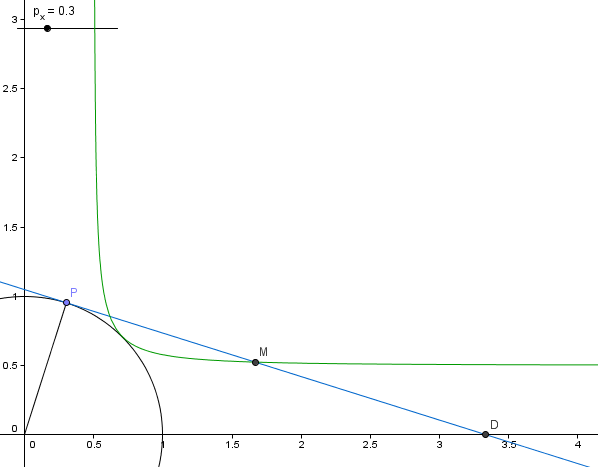
Ich habe dazu noch ein kleines Bild angefertigt, dass die Situation darstellt. Alle Bezeichnung sind wie in der Lösung gewählt.
In Blau die Tangente, in grün die beschriebene Kurve.
Durch Verschieben des Reglers für px kann ich im Programm (im Bild natürlich nicht) demonstrieren, dass der Punkt sich tatsächlich auf der Kurve bewegt.
Falls das übrigens eine Matheolympiade-Aufgabe ist, würde ich dir raten, dir die Lösung sehr genau anzusehen und nicht einfach nur so hinzunehmen. Das wird bei den späteren Aufgaben nicht unbedingt einfacher.