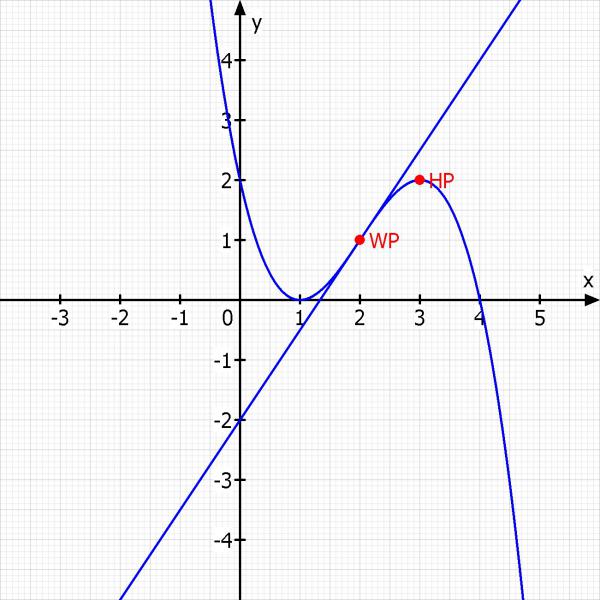
Eine Funktion 3. Grades
f(x) = a·x^3 + b·x^2 + c·x + d
f'(x) = 3·a·x^2 + 2·b·x + c
f''(x) = 6·a·x + 2·b
hat einen Hochpunkt bei H(3|2)
f(3) = 2 --> Du setzt 3 in die Funktionsgleichung ein und setzt das ganze gleich 2.
27·a + 9·b + 3·c + d = 2
f'(3) = 0
27·a + 6·b + c = 0
und an der Stelle Xw=2 eine Wendestelle.
f''(2) = 0
12·a + 2·b = 0
Die Wendetangente hat die Steigung 1,5.
f'(2) = 1.5
12·a + 4·b + c = 1.5
Wir erhalten ein lineares Gleichungssystem mit 4 Gleichungen und 4 Unbekannten.
27·a + 9·b + 3·c + d = 2
27·a + 6·b + c = 0
12·a + 2·b = 0
12·a + 4·b + c = 1.5
Das kannst du jetzt über das Additionsverfahren lösen.
Du solltest folgende Lösung bekommen: a = -0.5 ∧ b = 3 ∧ c = -4.5 ∧ d = 2
Demnach lautet die Funktionsgleichung: f(x) = -0.5·x^3 + 3·x^2 - 4.5·x + 2
Ich mache dir noch eine Skizze: