ich habe die Ungleichung ( x+a ) / (b-x )> 0
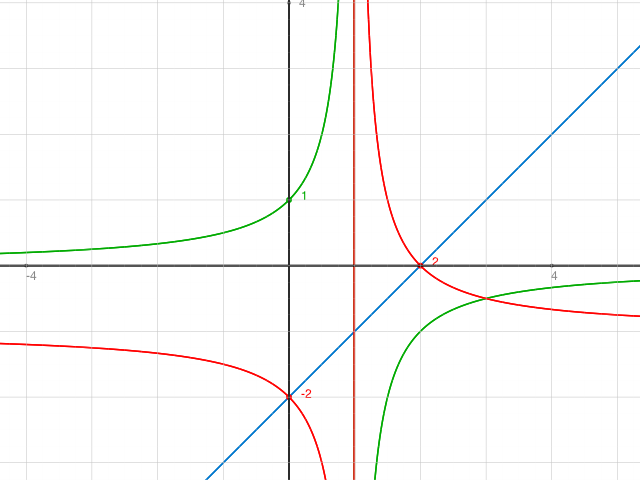
Hier mal ein Graph für y= (x+(-2)) / (1-x) (rot) inkl. y = x+(-2) (blau) und y= 1/(1-x) (grün)
Hier ist das Intervall (1,2) die Lösungsmenge der Ungleichung.
a) Bestimmen Sie a und b so, dass die Lösungsmenge der Ungleichung gleich dem Intervall (1,3) ist. Wie viele Paare a und b gibt es? Geometrische Begründung anhand der Funktionsgraphen von Zähler und Nenner.
Anpassen an die verlangte Menge y= (x+(-3)) / (1-x) D.h. a=-3 und b=1
Zähler y = x+(-3) ist eine Gerade, steigend, Vorzeichenwechsel in x=3, Nenner (1-x) Gerade, fallend, Vorzeichenwechsel in x=1
y= 1/(1-x) ist eine Hyperbel mit einfachem Pol mit Vorzeichenwechsel in x=1
Das Intervall (1,3) ist die Lösungsmenge der Ungleichung. (x+(-3)) / (1-x) > 0
b) Geben Sie alle a und b an, sodass die Ungleichung keine Lösung hat. (Leere Lösungsmenge) Wie viele Paare a und b. Geometrische Lösung
Hier fehlt ein Teil der Fragestellung.
y=(x + (-b)) / (b-x)
Also a = -b, beliebige reelle Zahlen. Es gibt also unendlich viele Paare (a,b) für die
(x+a)/(b-x) > 0 keine Lösung hat. L= {Paare (a,b)| a = -b}
c) a und b bestimmen dass die Lösungsmenge der Ungleichung gleich dem Halbstrahl (3,+unendlich) ist. Wie viele Paare a und b gibt es. Geometrische Lösung.
Das geht meiner Meinung nach nicht, da bei a≠b zwingend 2 Nulldurchgänge nötig sind.
Hier ein Beispiel.
Für a=0 und b=3 wäre die Lösungsmenge von (x+a)/(b-x) <0 = (-∞,0) u (3,∞)
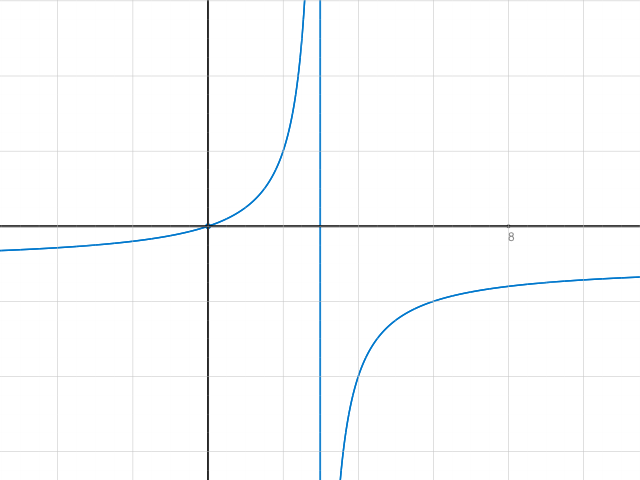
Ich habe nun herausgefunden, dass x+a eine Gerade richtig! ist und b-x nein! eine Kurve.
y=b-x ist ebenfalls eine Geradengleichung. y=1/(b-x) beschreibt eine Kurve.